题目内容
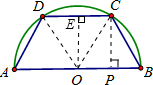
 如图,半径为2的圆内接等腰梯形ABCD,它的下底AB是圆的直径,上底CD的端点在圆周上,则该梯形周长的最大值是
如图,半径为2的圆内接等腰梯形ABCD,它的下底AB是圆的直径,上底CD的端点在圆周上,则该梯形周长的最大值是分析:根据圆心为O,则OA=OB=OC=OD=2,设腰长为x,设上底长是2b,利用勾股定理得出,则x2-(2-b)2=R2-b2=CP2,再利用二次函数最值求出即可.
解答:解:圆心为O,连接OD,OC,过O作OE⊥CD,过C作CP⊥OB,
∴E为DC的中点,DE=CE=
CD=b,
∵等腰梯形ABCD,
∴DC∥AB,OE⊥CD,
∴OE⊥AB,
∴∠CEO=∠EOP=∠OPC=90°,
∴四边形EOPC为矩形,
∴EC=OP,
则OA=OB=OC=OD=2,设腰长为x,
设上底长是2b,过C作直径的垂线,垂足是P,
则CP2=OC2-OP2=CB2-PB2,
即x2-(2-b)2=22-b2,
整理得b=2-
,
所以y=4+2x+2b=4+2x+4-
=-
+2x+8,
∴该梯形周长的最大值是:
=
=10.
故答案为:10.
∴E为DC的中点,DE=CE=
| 1 |
| 2 |
∵等腰梯形ABCD,
∴DC∥AB,OE⊥CD,
∴OE⊥AB,
∴∠CEO=∠EOP=∠OPC=90°,
∴四边形EOPC为矩形,
∴EC=OP,

则OA=OB=OC=OD=2,设腰长为x,
设上底长是2b,过C作直径的垂线,垂足是P,
则CP2=OC2-OP2=CB2-PB2,
即x2-(2-b)2=22-b2,
整理得b=2-
| x2 |
| 4 |
所以y=4+2x+2b=4+2x+4-
| x2 |
| 2 |
| x2 |
| 2 |
∴该梯形周长的最大值是:
| 4ac-b 2 |
| 4a |
| -16-4 |
| -2 |
故答案为:10.
点评:此题主要考查了二次函数的最值以及等腰梯形的性质和解直角三角形,根据题意得出x2-(2-b)2=R2-b2=CP2 从而利用二次函数最值求法求出是解决问题的关键.

练习册系列答案
相关题目
 如图,半径为2的圆内的点P到圆心O的距离为1,过点P的弦AB与劣弧组成一个弓形,则此弓形周长的最小值为( )
如图,半径为2的圆内的点P到圆心O的距离为1,过点P的弦AB与劣弧组成一个弓形,则此弓形周长的最小值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,半径为r1的圆内切于半径为r2的圆,切点为P,弦AB经过O1交⊙O1于C,D.已知AC:CD:DB=3:4:2,则
如图,半径为r1的圆内切于半径为r2的圆,切点为P,弦AB经过O1交⊙O1于C,D.已知AC:CD:DB=3:4:2,则 如图,半径为r1的圆内切于半径为r2的圆,切点为P,过圆心O1的直线与⊙O2交于A、B,与⊙O1交于C、D,已知AC:CD:DB=3:4:2,则
如图,半径为r1的圆内切于半径为r2的圆,切点为P,过圆心O1的直线与⊙O2交于A、B,与⊙O1交于C、D,已知AC:CD:DB=3:4:2,则