题目内容
方程
的解是 ________．
x1=19、x2=
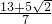、x3=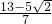
分析：把方程两边平方去根号，然后移项、合并同类项得7x3-159x2+511x-323=0，再分解因式得，（x-19）[x（7x-1）-（25x-17）]=0，最后解方程即可．
解答：将方程的两边平方，得
=
，
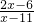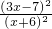化简，得
7x3-159x2+511x-323=0，
∴x（7x-1）（x-19）-（x-19）（25x-17）=0，
∴（x-19）[x（7x-1）-（25x-17）]=0，
∴x-19=0，或x（7x-1）-（25x-17）=0；
①当x-19=0时，解得x=19，
把x=19代入原式检验，左边=2，右边=2，所以，x=19是原方程的根；
②当x（7x-1）-（25x-17）=0时，即7x2-26x+17=0，
解得，x1=，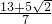
x2=；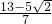
经检验，x1、x2是原方程的解．
故答案为：x1=19、x2=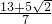、x3=．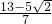
点评：在解无理方程是最常用的方法是两边平方法及换元法，本题用了平方法．
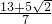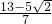
、x3=分析：把方程两边平方去根号，然后移项、合并同类项得7x3-159x2+511x-323=0，再分解因式得，（x-19）[x（7x-1）-（25x-17）]=0，最后解方程即可．
解答：将方程的两边平方，得
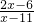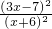=，化简，得
7x3-159x2+511x-323=0，
∴x（7x-1）（x-19）-（x-19）（25x-17）=0，
∴（x-19）[x（7x-1）-（25x-17）]=0，
∴x-19=0，或x（7x-1）-（25x-17）=0；
①当x-19=0时，解得x=19，
把x=19代入原式检验，左边=2，右边=2，所以，x=19是原方程的根；
②当x（7x-1）-（25x-17）=0时，即7x2-26x+17=0，
解得，x1=
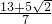，x2=
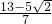；经检验，x1、x2是原方程的解．
故答案为：x1=19、x2=
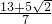、x3=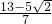．点评：在解无理方程是最常用的方法是两边平方法及换元法，本题用了平方法．
练习册系列答案
全能测控期末小状元系列答案
相关题目
某二元方程的解是
，若把x看作平面直角坐标系中点的横坐标，y看作平面直角坐标系中点的纵坐标，下面说法正确的是（ ）
|
| A、点（x，y）一定不在第一象限 |
| B、点（x，y）一定不是坐标原点 |
| C、y随x的增大而增大 |
| D、y随x的增大而减小 |