题目内容
已知正方形ABCD的边长为4,E是CD上一个动点,以CE为一条直角边作等腰直角三角形CEF,连接BF、BD、FD.
(1)BD与CF的位置关系是________.
(2)①如图,当CE=4(即点E与点D重合)时,△BDF的面积为________.
②如图,当CE=2(即点E为CD中点)时,△BDF的面积为________.
③如图,当CE=3时,△BDF的面积为________.
(3)如图,根据上述计算的结果,当E是CD上任意一点时,请提出你对 △BDF面积与正方形ABCD的面积之间关系的猜想,并证明你的猜想.
△BDF面积与正方形ABCD的面积之间关系的猜想,并证明你的猜想.
解:(1)正方形ABCD,等腰直角三角形CEF,
∴∠ADC=∠FDC=90°,
∴∠ADC+∠FDC=180°,
即A、D、F三点共线,
∵DF∥CB,DF=CD=BC,
∴四边形BCFD是平行四边形,
∴FC∥BD,
故答案为:平行.
(2)①△BDF的面积是 DF×AB=
DF×AB= ×4×4=8,
×4×4=8,
故答案为:8.
②△BDF的面积是:S四边形BCFD-S△BCF
=S△BDC+S△CDF-S△BCF
= BC×DC+
BC×DC+ CD×EF-
CD×EF- BC×CE
BC×CE
= ×4×+
×4×+ ×4×2-
×4×2- ×4×2
×4×2
=8,
故答案为:8.
③与②求法类似:△BDF的面积是S△BDC+S△CDF-S△BCF
= BC×CD+
BC×CD+ CD×EF-
CD×EF- CB×EF
CB×EF
= ×4×4+
×4×4+ ×4×3-
×4×3- ×4×3
×4×3
=8,
故答案为:8.
(3)△BDF面积与正方形ABCD的面积之间关系是S△BDF= S正方形ABCD.
S正方形ABCD.
证明:∵S△BDF=8,
S正方形ABCD=BC×CD=4×4=16,
∴S△BDF= S正方形ABCD.
S正方形ABCD.
分析:(1)证A、D、F共线,根据平行四边形的判定推出平行四边形BCFD即可;
(2)①根据三角形的面积公式求出即可;②③根据S△BDF=S四边形BCDF-S△BCF=S△BCD+S△CDF-S△BCF代入求出即可;
(3)由(2)求出了△BDF的面积,求出正方形的面积,即可得出答案.
点评:本题综合考查了正方形的性质,三角形的面积,等腰直角三角形,平行四边形的性质和判定等知识点的应用,解此题的关键是把要求的三角形的面积转化成能根据已知求出的三角形的面积的和或差的形式,再根据三角形的面积公式求出每一部分的面积.
∴∠ADC=∠FDC=90°,
∴∠ADC+∠FDC=180°,
即A、D、F三点共线,
∵DF∥CB,DF=CD=BC,
∴四边形BCFD是平行四边形,
∴FC∥BD,
故答案为:平行.
(2)①△BDF的面积是
 DF×AB=
DF×AB= ×4×4=8,
×4×4=8,故答案为:8.
②△BDF的面积是:S四边形BCFD-S△BCF
=S△BDC+S△CDF-S△BCF
=
 BC×DC+
BC×DC+ CD×EF-
CD×EF- BC×CE
BC×CE=
 ×4×+
×4×+ ×4×2-
×4×2- ×4×2
×4×2=8,
故答案为:8.
③与②求法类似:△BDF的面积是S△BDC+S△CDF-S△BCF
=
 BC×CD+
BC×CD+ CD×EF-
CD×EF- CB×EF
CB×EF=
 ×4×4+
×4×4+ ×4×3-
×4×3- ×4×3
×4×3=8,
故答案为:8.
(3)△BDF面积与正方形ABCD的面积之间关系是S△BDF=
 S正方形ABCD.
S正方形ABCD.证明:∵S△BDF=8,
S正方形ABCD=BC×CD=4×4=16,
∴S△BDF=
 S正方形ABCD.
S正方形ABCD.分析:(1)证A、D、F共线,根据平行四边形的判定推出平行四边形BCFD即可;
(2)①根据三角形的面积公式求出即可;②③根据S△BDF=S四边形BCDF-S△BCF=S△BCD+S△CDF-S△BCF代入求出即可;
(3)由(2)求出了△BDF的面积,求出正方形的面积,即可得出答案.
点评:本题综合考查了正方形的性质,三角形的面积,等腰直角三角形,平行四边形的性质和判定等知识点的应用,解此题的关键是把要求的三角形的面积转化成能根据已知求出的三角形的面积的和或差的形式,再根据三角形的面积公式求出每一部分的面积.

练习册系列答案
相关题目
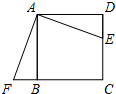 如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为
如图,已知正方形ABCD的边长为12cm,E为CD边上一点,DE=5cm.以点A为中心,将△ADE按顺时针方向旋转得△ABF,则点E所经过的路径长为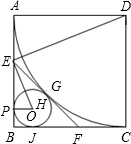 合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H
合),过点E作弧AC的切线,交BC于点F,G为切点,⊙O是△EBF的内切圆,分别切EB、BF、FE于点P、J、H (2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(2011•同安区质检)如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. (2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒.
(2012•香洲区一模)如图,已知正方形ABCD的边长为28,动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动(点P到达点D时终止运动),动直线EF从AD开始以每秒1个单位长度的速度向下平行移动(即EF∥AD),并且分别与DC、AC交于E、F两点,连接FP,设动点P与动直线EF同时出发,运动时间为t 秒. 如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是
如图,已知正方形ABCD的边长为8cm,点E、F分别在边BC、CD上,∠EAF=45°.当EF=8cm时,△AEF的面积是