题目内容
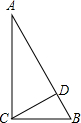
如图，直角三角形ABC中，O是BC中点且BD⊥CD，试说明AO与OD的关系．
解：AO=DO，
理由是：∵∠BAC=90°，O为BC中点，
∴AO=
BC，
∵BD⊥CD，
∴∠BDC=90°，
∵O为BC中点，
∴DO=BC，
∴AO=DO，
分析：根据直角三角形斜边上中线等于斜边的一半得出AO=BC，同理DO=BC，即可推出答案．
点评：本题考查了直角三角形斜边上中线性质的应用，题目比较典型，难度不大．
理由是：∵∠BAC=90°，O为BC中点，
∴AO=
BC，∵BD⊥CD，
∴∠BDC=90°，
∵O为BC中点，
∴DO=
BC，∴AO=DO，
分析：根据直角三角形斜边上中线等于斜边的一半得出AO=
BC，同理DO=BC，即可推出答案．点评：本题考查了直角三角形斜边上中线性质的应用，题目比较典型，难度不大．
练习册系列答案
相关题目
如图，直角三角形ABC中∠ACB=90°，CD是高，∠A=30°，AB=4．则BD=
如图，直角三角形ABC的直角边AB=6，以AB为直径画半圆，若阴影部分的面积S1-S2=
如图在直角三角形ABC的斜边AB上另作直角三角形ABD，并以AB为斜边，若BC=1，AC=m，AD=2，则BD等于（ ）
如图，直角三角形ACB中，CD是斜边AB上的中线，若AC=8cm，BC=6cm，那么△ACD与△BCD的周长差为
如图，直角三角形ABC中，∠C=90°，P，E分别是边AB，BC上的点，D为△ABC外一点，DE⊥BC，DE=EC，BE=2EC，∠BDE=∠PEC，AD∥PE，AC=4，则线段BC的长为