题目内容
如图,?ABCD中,E、F分别为AD、BC上的点,且DE=2AE,BF=2FC,连接BE、AF交于点H,连接DF、CE交于点G,则 = .
= .
【答案】分析:根据DE=2AE,BF=2FC,找出各边的比值,然后利用三角形和平行四边形的面积公式求解即可.
解答:解:∵DE=2AE,BF=2FC,
∴BF=2AE,ED=2CF,
即有△AHE∽△FHB,△CFG∽△EGD,
则 =
= ,同理
,同理 =
=
∴S△BFH= S△ABF=
S△ABF= ×
× ×
× ×S?ABCD,
×S?ABCD,
S△CFG= S△CFD=
S△CFD= ×
× S?ABCD,
S?ABCD,
故S四边形EHFG=S△BCE-S△BFH-S△CFG= S?ABCD-
S?ABCD- S?ABCD
S?ABCD S?ABCD=
S?ABCD= S?ABCD.
S?ABCD.
故答案为:
点评:本题考查平行四边形的性质及相似三角形的判定与性质,难度适中,解题关键是熟练掌握并灵活应用三角形和平行四边形的面积公式.
解答:解:∵DE=2AE,BF=2FC,
∴BF=2AE,ED=2CF,
即有△AHE∽△FHB,△CFG∽△EGD,
则
 =
= ,同理
,同理 =
=
∴S△BFH=
 S△ABF=
S△ABF= ×
× ×
× ×S?ABCD,
×S?ABCD,S△CFG=
 S△CFD=
S△CFD= ×
× S?ABCD,
S?ABCD,故S四边形EHFG=S△BCE-S△BFH-S△CFG=
 S?ABCD-
S?ABCD- S?ABCD
S?ABCD S?ABCD=
S?ABCD= S?ABCD.
S?ABCD.故答案为:

点评:本题考查平行四边形的性质及相似三角形的判定与性质,难度适中,解题关键是熟练掌握并灵活应用三角形和平行四边形的面积公式.

练习册系列答案
相关题目
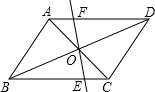 如图,?ABCD中,AB⊥AC,AB=1,BC=
如图,?ABCD中,AB⊥AC,AB=1,BC=| 5 |
| A、当旋转角为90°时,四边形ABEF一定为平行四边形 |
| B、在旋转的过程中,线段AF与EC总相等 |
| C、当旋转角为45°时,四边形BEDF一定为菱形 |
| D、当旋转角为45°时,四边形ABEF一定为等腰梯形 |
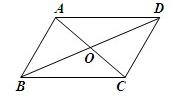 9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )
9、如图,?ABCD中,O为AC、BD的中点,则图中全等的三角形共有( )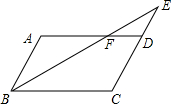 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=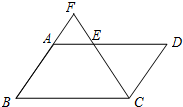 已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F.
已知:如图,?ABCD中,点E是AD的中点,延长CE交BA的延长线于点F. (1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为
(1997•浙江)如图,?ABCD中,对角线AC和BD交于点O,过O作OE∥BC交DC于点E,若OE=5cm,则AD的长为