题目内容
有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形(所有正多边形的边长相等),把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.

(1)请你用画树形图或列表的方法列举出可能出现的所有结果;
(2)如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形能构成平面镶嵌的概率;
(3)若两种正多边形构成平面镶嵌,p、q表示这两种正多边形的个数,x、y表示对应正多边形的每个内角的度数,则有方程px+qy=360,求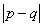 的值
的值
解:(1)画树形图如下:

所有出现的结果共有12种。…………3分
(2)∵两次抽取的正多边形能构成平面镶嵌的情况有4种:AB,AD,BA,DA,
∴P(两次抽取的正多边形能构成平面镶嵌)=
(3)当正三角形和正方形构成平面镶嵌时,则有60p+90q=360,即2p+3q=12
∵p、q是正整数,∴p=3,q=2…………1分
当正三角形和六边形构成平面镶嵌时,则有60p+120q=360,即p+2q=6。
∵p、q是正整数,∴p=4,q=1或p=2,q=2
∴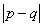 =1或3或0
=1或3或0
(酌情给分)

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
从1到9这九个自然数中任取一个,是奇数的概率是( )
|
| A. |
| B. |
| C. |
| D. |
|
萧山素以“萝卜干之乡”著称.某乡组织20辆汽车装运A、B、C三种不同包装的萝卜干42吨到外地销售.按规定每辆车只装同一种萝卜干,且必须装满,每种萝卜干不少于2车.
设有x辆车装运A种萝卜干,用y辆车装运B种萝卜干,根据下表提供的信息,求y与x之间的函数关系,并求x的取值范围;
设此次外销活动的利润为W(百元),求W与x的函数关系式以及最大利润,并安排相应的车辆分配方案.
| 萝卜干品种 | A | B | C |
| 每辆汽车运载量(吨) | 2.2 | 2.1 | 2 |
| 每吨萝卜干获利(百元) | 6 | 8 | 5 |
 (2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB=
(2)在⊿ABC中作BC的中垂线分别交AB、BC于点M、N,如果SinB= ,求⊿BMN与⊿ABC的面积之比。
,求⊿BMN与⊿ABC的面积之比。 中,
中, 为⊙
为⊙ 的直径,
的直径, ,则sin
,则sin =____________
=____________
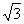 B.
B. 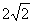 C. 2
C. 2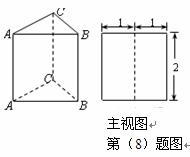
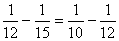 ,此时我们称15,12,10为一组调和数,现有三个数:5,3,x(
,此时我们称15,12,10为一组调和数,现有三个数:5,3,x(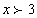 ),若要组成调和数,则x的值为___________
),若要组成调和数,则x的值为___________ ,
, ,∴
,∴ ;∵
;∵ ,
, ,∴
,∴ ,由此猜想、推理知:一般地当
,由此猜想、推理知:一般地当 为锐角时有
为锐角时有 ,由此可知:
,由此可知: ( )
( )  B.
B. C.
C. D.
D.



