题目内容
 如图,点K、B、C分别在GH、GA、KA上,且AB=AC,BG=BH,KA=KG,求∠BAC的度数.
如图,点K、B、C分别在GH、GA、KA上,且AB=AC,BG=BH,KA=KG,求∠BAC的度数.分析:设∠A=x,根据等边对等角的性质可得∠G=∠A,∠H=∠G,∠ABC=∠ACB,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ABC=∠G+∠H,然后根据三角形的内角和定理列式计算即可得解.
解答:解:设∠A=x,
∵KA=KG,
∴∠G=∠A=x,
∵BG=BH,
∴∠H=∠G=x,
由三角形的外角性质,∠ABC=∠G+∠H=2x,
∵AB=AC,
∴∠ABC=∠ACB=2x,
在△ABC中,∠A+∠ABC+∠ACB=180°,
∴x+2x+2x=180°,
解得x=36°,
即∠BAC=36°.
∵KA=KG,
∴∠G=∠A=x,
∵BG=BH,
∴∠H=∠G=x,
由三角形的外角性质,∠ABC=∠G+∠H=2x,
∵AB=AC,
∴∠ABC=∠ACB=2x,
在△ABC中,∠A+∠ABC+∠ACB=180°,
∴x+2x+2x=180°,
解得x=36°,
即∠BAC=36°.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,准确识图找准各角度之间的关系是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
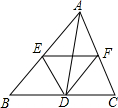
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、EF与AD互相平分 | ||
B、EF=
| ||
| C、AD平分∠BAC | ||
| D、△DEF∽△ACB |
 如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )
如图,点D,E,F分别是△ABC(AB>AC)各边的中点,下列说法中,错误的是( )| A、AD平分∠BAC | ||
B、EF=
| ||
| C、EF与AD互相平分 | ||
| D、△DFE是△ABC的位似图形 |
 5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件:
5、如图,点D、E、F分别是△ABC的边AB、BC、AC的中点,连接DE、EF,要使四边形ADEF为正方形,还需增加条件: 如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是
如图,点D,E,F分别是△ABC的三边AB,AC,BC上的中点,如果△ABC的面积是18cm2,则△DBF的面积是 如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )
如图,点D、E、F分别是△ABC三边AB、BC、AC的中点,则△DEF的周长是△ABC周长的( )