题目内容
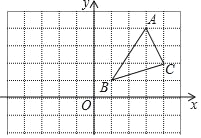
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
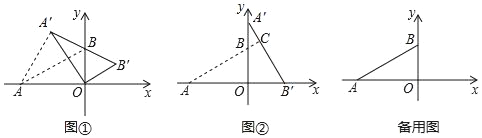
(1)如图①,当点A′,B,B′共线时,求AA′的长.
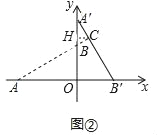
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
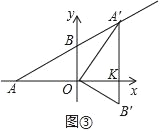
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
【答案】(1)AA′=![]() ;(2)(
;(2)(![]() ,
,![]() );(3)(
);(3)(![]() ,
,![]() ).
).
【解析】
(1)如图①,只要证明△AOA′是等边三角形即可;
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.解直角三角形求出BH,CH即可解决问题;
(3)如图③,设A′B′交x轴于点K.首先证明A′B′⊥x轴,求出OK,A′K即可解决问题;
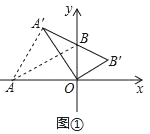
(1)如图①,
∵A(﹣![]() ,0),B(0,1),
,0),B(0,1),
∴OA=![]() ,OB=1,
,OB=1,
∴tan∠BAO=![]() ,
,
∴∠BAO=30°,∠ABO=60°,
∵△A′OB′是由△AOB旋转得到,
∴∠B′=∠ABO=60°,OB=OB′,OA=OA′,
∴∠OBB′=60°,
∴∠BOB′=α=∠AOA′=60°,
∴△AOA′是等边三角形,
∴AA′=OA=![]() .
.
(2)如图②,当α=90°,点A′在y轴上,作CH⊥OA′于H.
∵∠A′B′O=60°,∠CAB′=30°,
∴∠ACB′=90°,
∵A′B=OA′﹣OB=![]() ﹣1,∠BA′C=30°,
﹣1,∠BA′C=30°,
∴BC=![]() A′B=
A′B=![]() ,
,
∵∠HBC=60°,
∴BH=![]() BC=
BC=![]() ,CH=
,CH=![]() BH=
BH=![]() ,
,
∴OH=1+BH=![]() ,
,
∴点C的坐标(![]() ,
,![]() ).
).
(3)如图③中,设A′B′交x轴于点K.
当A′在AB上时,∵OA=OA′,
∴∠OAA′=∠AA′O=30°,
∵∠OA′B′=30°,
∴∠AA′K=60°,
∴∠AKA′=90°,
∵OA′=![]() ,∠OA′K=30°,
,∠OA′K=30°,
∴OK=![]() OA′=
OA′=![]() ,A′K=
,A′K=![]() OK=
OK=![]() ,
,
∴A′(![]() ,
,![]() ).
).

 科学实验活动册系列答案
科学实验活动册系列答案