题目内容
在Rt△ABC中,∠CAB=90°,AB=AC.
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM=a,BM=b,AB=c,试利用图①验证勾股定理a2+b2=c2;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)
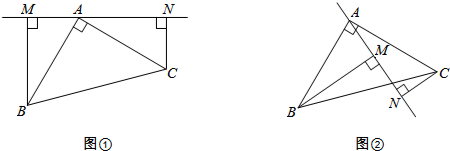
(1)如图①,过点A在△ABC外作直线MN,BM⊥MN于M,CN⊥MN于N.
①判断线段MN、BM、CN之间有何数量关系,并证明;
②若AM=a,BM=b,AB=c,试利用图①验证勾股定理a2+b2=c2;
(2)如图②,过点A在△ABC内作直线MN,BM⊥MN于M,CN⊥MN于N,判断线段MN、BM、CN之间有何数量关系?(直接写出答案)

分析:(1)①利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系;
②利用S梯形MBCN=S△MAB+S△ABC+S△NCA=
ab+
c2+
ab,S梯形MBCN=
(BM+CN)×MN=
(a+b)2,进而得出答案;
(2)利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系.
②利用S梯形MBCN=S△MAB+S△ABC+S△NCA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用已知得出∠MAB=∠ACN,进而得出△MAB≌△NCA,进而得出BM=AN,AM=CN,即可得出线段MN、BM、CN之间的数量关系.
解答:解: (1)①MN=BM+CN;
(1)①MN=BM+CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
,
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AM+AN=BM+CN;
②由①知△MAB≌△NCA,
∴CN=AM=a,AN=BM=b,AC=BC=c,
∴MN=a+b,
∵S梯形MBCN=S△MAB+S△ABC+S△NCA=
ab+
c2+
ab,
S梯形MBCN=
(BM+CN)×MN=
(a+b)2,
∴
ab+
c2+
ab=
(a+b)2,
∴a2+b2=c2;
(2)MN=BM-CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
,
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AN-AM=BM-CN.
 (1)①MN=BM+CN;
(1)①MN=BM+CN;理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
|
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AM+AN=BM+CN;
②由①知△MAB≌△NCA,
∴CN=AM=a,AN=BM=b,AC=BC=c,
∴MN=a+b,
∵S梯形MBCN=S△MAB+S△ABC+S△NCA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S梯形MBCN=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴a2+b2=c2;
(2)MN=BM-CN;
理由:∵∠MAB+∠NAC=90°,∠ACN+∠NAC=90°,
∴∠MAB=∠ACN,
在△MAB和△NCA中
|
∴△MAB≌△NCA(AAS),
∴BM=AN,AM=CN,
∴MN=AN-AM=BM-CN.
点评:此题主要考查了全等三角形的判定与性质以及勾股定理的证明等知识,根据已知得出△MAB≌△NCA是解题关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
在Rt△ABC中,已知a及∠A,则斜边应为( )
| A、asinA | ||
B、
| ||
| C、acosA | ||
D、
|
 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC的值为( )| A、9:4 | B、9:2 | C、3:4 | D、3:2 |
 已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径.
已知:如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于E,求⊙O的半径. 如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )
如图,已知:在Rt△ABC中,∠C=90°,AB=12,点D是AB的中点,点O是△ABC的重心,则OD的长为( )