Question

【题目】阅读材料：

①直线l外一点P到直线l的垂线段的长度，叫做点P到直线l的距离，记作d（P，l）；

②两条平行线，，直线上任意一点到直线的距离，叫做这两条平行线，之间的距离，记作d（，）；

③若直线，相交，则定义d（，）=0；

④若直线，重合，我们定义d（，）=0，

对于两点，和两条直线，，定义两点，的“，相关距离”如下：

d（，|，）=d（，）+d（，）+d（，）

设（4，0），（0，3），：y=x，：y=，：y=kx，解决以下问题：

（1）d（，|，）= ；

（2）①若k＞0，则当d（，|，）最大时，k= ；

②若k＜0，试确定k的值，使得d（，|，）最大，请说明理由．

Answer 1

【答案】(1) ；(2)①；②.

【解析】

试题分析：（1）首先分别求出d（，）、d（，）、d（，）的值各是多少，再把它们求和，求出d（，|，）的值是多少；然后分别求出d（，）、d（，）、d（，）的值各是多少，再把它们求和，求出d（，|，）的值是多少即可．

（2）①首先作A⊥于点A，B⊥于点B，连接交于点C，然后根据A+B≤，可得当⊥时，A+B的值最大，据此求出k的值是多少即可．

②首先作A⊥于点A，B⊥于点B，、关于原点对称，C⊥于点C，交于点D，然后根据B+C≤，可得当⊥时，B+C取到最大值，据此求出k的值是多少即可．

试题解析：（1）∵（4，0），（0，3），：y=x，：y=，

∴d（，|，）=d（，）+d（，）+d（，）==；

∴d（，|，）= d（，）+d（，）+d（，）==.

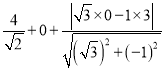故答案为：；

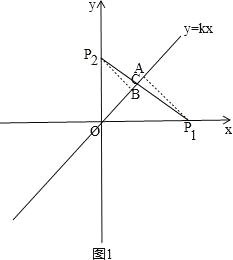
（2）①如图1，作A⊥于点A，B⊥于点B，连接交于点C，

d（，|，）=d（，）+d（，）+d（，）=A+B，

∵A≤C，B≤C，

∴A+B≤，

∴当⊥时，

A+B的最大值是：=5，

此时k=tan∠O==，

∴若k＞0，当d（，|，）最大时，k=．

故答案为：；

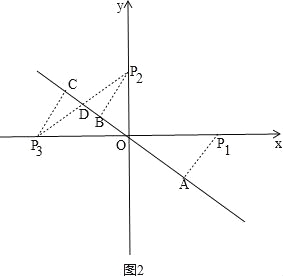
②如图2，作A⊥于点A，B⊥于点B，、关于原点对称，C⊥于点C，交于点D，

∵、关于原点对称，

∴A=C，

∴d（，|，）=d（，）+d（，）+d（，）=A+B=B+C，

∵B≤D，C≤D，

∴B+C≤，

∴当⊥时，

B+C的最大值是：==5，

此时k=﹣tan∠O==，

∴若k＜0，当d（，|，）最大时，k=．