Question

【题目】在平面直角坐标系中，已知两点A(-4,0)、B(1,0)，且以AB为直径的圆交轴的正半轴于点C(0，2)，过点C作圆的切线交x轴于点D．

（1）求过A, B,C三点的抛物线解析式；

（2）求点D的坐标；

（3）设平行于x轴的直线交抛物线于E,F两点，问是否存在以线段EF为直径的圆，恰好与x轴相切？若存在，求出该圆的半径，若不存在，请说明理由.

Answer 1

【答案】（1）;(2)D的坐标为（，0）;（3）存在, 或．

【解析】（1）已知了抛物线过A，B，C三点，可根据三点的坐标用待定系数法求出抛物线的解析式．
（2）由于CD是圆的切线，设圆心为O′，可连接O′C，在直角三角形O′CD中科根据射影定理求出OD的长，即可得出D的坐标．
（3）可假设存在这样的点E、F，设以线段EF为直径的圆的半径为|r|，那么可用半径|r|表示出E，F两点的坐标，然后根据E，F在抛物线上，将E，F的坐标代入抛物线的解析式中，可得出关于|r|的方程，如果方程无解则说明不存在这样的E，F点，如果方程有解，可用得出的r的值求出E，F两点的坐标．

解：（1）设二次函数的解析式为，则

， ，

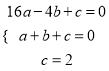故抛物线的解析式为 ．

过圆心O′做抛物线的对称轴，连接O′C.

（2）如图所示，

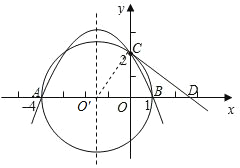
以为直径的圆圆心坐标为O′（，0）．

， ．

∵CD为⊙O′切线
∴O′C⊥CD，

∵ ∠O′OC=∠COD=90°

∴ ∠CDO+∠DCO=∠CDO+∠CO′O=90°

∴ ∠DCO=∠CO′O

∴ ⊿O′CO∽⊿CDO, ,

∴,

．

∴ D的坐标为（，0）．

（3）存在．抛物线对称轴为．设圆的半径为r(r>0)，令点在点F的左边．

①当E,F在轴上方时，则E坐标为（-r,r）,F坐标为（+r,r）将点E坐标代入抛物线

中，得r= (-r)2- (--r)+2，

， （舍去）．

②当E，F在x轴下方时，则E坐标为（--r,-r）,F坐标为(-+r,-r)，将E点的坐标代入 ．得-r=-(--r)2- (--r)+2，得r3=1+或r4=1- (舍去) ．

故在以为直径的圆，恰好与轴相切，该圆的半径为或．

“点睛”本题着重考查了待定系数法求二次函数解析式、三角形相似、切线的性质等重要知识点，综合性强，考查学生数形结合的数学思想方法．