��Ŀ����
��֪������C1��y=a��x+1��2��2�Ķ���ΪA���Ҿ�����B����2����1����
��1����A��������������C1�Ľ���ʽ��
��2����ͼ1����������C1����ƽ��2����λ��õ�������C2����������C2��ֱ��AB�ཻ��C��D���㣬��S��OAC��S��OAD��ֵ��
��3����ͼ2������P����4��0����Q��0��2����ֱ��Ϊl����E�ڣ�2����������C2�Գ����Ҳಿ�֣������㣩�˶���ֱ��m����C�͵�E���ʣ��Ƿ����ֱ��m��ʹֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ������ڣ����ֱ��m�Ľ���ʽ���������ڣ�˵�����ɣ�


��
�����㡿���κ����ۺ��⣻����ϵ������һ�κ�������ʽ������ϵ��������κ�������ʽ�����������ε��ж������ʣ�������Ǻ����������ԣ�
��ר�⡿ѹ���⣻�����ͣ�
����������1���������ߵĶ���ʽ�ö���A���꣬�ѵ�B��������������ߵĽ���ʽ���ɽ�����⣮
��2������ƽ�Ʒ������������C2�Ľ���ʽ���ô���ϵ�������ֱ��AB�Ľ���ʽ����ͨ���ⷽ�������������C2��ֱ��AB�Ľ���C��D�����꣬�Ϳ������S��OAC��S��OAD��ֵ��
��3����ֱ��m��y�ύ�ڵ�G��ֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ���������״��λ�����ŵ�G�ı仯���仯������Ե�G��λ�ý������ۣ����������������ε��ж������ʡ����Ǻ����������Ե�֪ʶ������������ĵ�G�����꣬�Ӷ������Ӧ��ֱ��m�Ľ���ʽ��
����𡿽⣺��1����������C1��y=a��x+1��2��2�Ķ���ΪA��
���A����������1����2����
��������C1��y=a��x+1��2��2������B����2����1����
��a����2+1��2��2=��1��
��ã�a=1��
��������C1�Ľ���ʽΪ��y=��x+1��2��2��
��2����������C2����������C1����ƽ��2����λ���ã�
��������C2�Ľ���ʽΪ��y=��x+1��2��2��2=��x+1��2��4��
��ֱ��AB�Ľ���ʽΪy=kx+b��
��A����1����2����B����2����1����
��

��ã�

��ֱ��AB�Ľ���ʽΪy=��x��3��
����

��ã�
 ��
��
 ��
��
��C����3��0����D��0����3����
��OC=3��OD=3��
����A��AE��x�ᣬ����ΪE��
����A��AF��y�ᣬ����ΪF��
��A����1����2����
��AF=1��AE=2��
��S��OAC��S��OAD
=��
 OC•AE������
OC•AE������
 OD•AF��
OD•AF��
=��
 ��3��2������
��3��2������
 ��3��1��
��3��1��
=2��
��S��OAC��S��OAD��ֵΪ2��
��3����ֱ��m��y�ύ�ڵ�G�����G������Ϊ��0��t����
1����ֱ��m��ֱ��lƽ��ʱ������CG��PQ��
���OCG�ס�OPQ��
��
 =
=
 ��
��
��P����4��0����Q��0��2����
��OP=4��OQ=2��
��
 =
=
 ��
��
��OG=
 ��
��
�ߵ�t=
 ʱ��ֱ��m��ֱ��lƽ�У�
ʱ��ֱ��m��ֱ��lƽ�У�
��ֱ��l��m��x��ܹ��������Σ�
��t��
 ��
��
2����ֱ��m��ֱ��l�ཻʱ���轻��ΪH��
��t��0ʱ����ͼ2����ʾ��
�ߡ�PHC����PQG����PHC����QGH��
���PHC�١�PQG����PHC�١�QGH��
����PHC=��GHQʱ��
�ߡ�PHC+��GHQ=180�㣬
���PHC=��GHQ=90�㣮
�ߡ�POQ=90�㣬
���HPC=90�㩁��PQO=��HGQ��
���PHC�ס�GHQ��
�ߡ�QPO=��OGC��
��tan��QPO=tan��OGC��
��
 =
=
 ��
��
��
 =
=
 ��
��
��OG=6��
���G��������0����6��
��ֱ��m�Ľ���ʽΪy=mx+n��
�ߵ�C����3��0������G��0����6����ֱ��m�ϣ�
��
 ��
��
��ã�
 ��
��
��ֱ��m�Ľ���ʽΪy=��2x��6��
����
 ��
��
��ã�
 ��
��

��E����1����4����
��ʱ��E���������ߵĶ��㣬����������
��ֱ��m�Ľ���ʽΪy=��2x��6��
�ڵ�t=0ʱ��
��ʱֱ��m��x���غϣ�
��ֱ��l��m��x��ܹ��������Σ�
��t��0��
��O��t��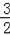
 ʱ����ͼ2����ʾ��
ʱ����ͼ2����ʾ��
��tan��GCO=
 =
=
 ��
��
 ��
��
tan��PQO=
 =
=
 =2��
=2��
��tan��GCO��tan��PQO��
���GCO�١�PQO��
�ߡ�GCO=��PCH��
���PCH�١�PQO��
�֡ߡ�HPC����PQO��
���PHC���GHQ�����ƣ�
�����������ֱ��m�����ڣ�
��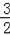
 ��t��2ʱ����ͼ2����ʾ��
��t��2ʱ����ͼ2����ʾ��
��tan��CGO=
 =
=
 ��
��
 ��
��
tan��QPO=
 =
=
 =
=
 ��
��
��tan��CGO��tan��QPO��
���CGO�١�QPO��
�ߡ�CGO=��QGH��
���QGH�١�QPO��
�֡ߡ�HQG����QPO��
���PHC���GHQ�����ƣ�
�����������ֱ��m�����ڣ�
��t��2ʱ����ͼ2����ʾ��
��ʱ��E�ڶԳ�����Ҳ࣮
�ߡ�PCH����CGO��
���PCH�١�CGO��
����QPC=��CGOʱ��
�ߡ�PHC=��QHG����HPC=��HGQ��
���PCH�ס�GQH��
�����������ֱ��m���ڣ�
�ߡ�QPO=��CGO����POQ=��GOC=90�㣬
���POQ�ס�GOC��
��
 =
=
 ��
��
��
 =
=
 ��
��
��OG=6��
���G��������0��6����
��ֱ��m�Ľ���ʽΪy=px+q
�ߵ�C����3��0������G��0��6����ֱ��m�ϣ�
��
 ��
��
��ã�
 ��
��
��ֱ��m�Ľ���ʽΪy=2x+6��
��������������ֱ��m��ʹֱ��l��m��x��Χ�ɵ������κ�ֱ��l��m��y��Χ�ɵ����������ƣ�
��ʱֱ��m�Ľ���ʽΪy=��2x��6��y=2x+6��










�����������⿼���˶��κ������й�֪ʶ�����������������Ƶ��ж������ʡ����Ǻ����Ķ��弰�����Ե�֪ʶ���������ô���ϵ��������κ�����һ�κ����Ľ���ʽ��������ͨ���ⷽ��������������ͼ��Ľ��㣬ǿ���˶�����������������ʶ����������˼��Ŀ��飬���н�ǿ���ۺ��ԣ���һ�����Ѷȣ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� ��2•
��2• +
+ ��
�� ��
��