题目内容
 (2013•上海)在矩形ABCD中,点P是边AD上的动点,连接BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,联结QP(如图).已知AD=13,AB=5,设AP=x,BQ=y.
(2013•上海)在矩形ABCD中,点P是边AD上的动点,连接BP,线段BP的垂直平分线交边BC于点Q,垂足为点M,联结QP(如图).已知AD=13,AB=5,设AP=x,BQ=y.(1)求y关于x的函数解析式,并写出x的取值范围;
(2)当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时,求x的值;
(3)点E在边CD上,过点E作直线QP的垂线,垂足为F,如果EF=EC=4,求x的值.
分析:(1)利用相似三角形△ABP∽△MQB,求出y关于x的函数解析式;注意求x的取值范围时,需考虑计算x最大值与最小值的情形;
(2)如答图1所示,利用相外切两圆的性质,求出PQ的长;利用垂直平分线的性质PQ=BQ,列方程求出x的值;
(3)如答图2所示,关键是证明△CEQ∽△ABP,据此列方程求出x的值.
(2)如答图1所示,利用相外切两圆的性质,求出PQ的长;利用垂直平分线的性质PQ=BQ,列方程求出x的值;
(3)如答图2所示,关键是证明△CEQ∽△ABP,据此列方程求出x的值.
解答:解:(1)在Rt△ABP中,由勾股定理得:BP2=AP2+AB2=x2+25.
∵MQ是线段BP的垂直平分线,
∴BQ=PQ,BM=
BP,∠BMQ=90°,
∴∠MBQ+∠BQM=90°,
∵∠ABP+∠MBQ=90°,∴∠ABP=∠BQM,
又∵∠A=∠BMQ=90°,
∴△ABP∽△MQB,
∴
=
,即
=
,化简得:y=
BP2=
(x2+25).
当点Q与C重合时,BQ=PQ=13,在Rt△PQD中,由勾股定理定理得:PQ2=QD2+PD2,即132=52+(13-x)2,解得x=1;
又AP≤AD=13,∴x的取值范围为:1≤x≤13.
∴y=
(x2+25)(1≤x≤13).
(2)当⊙P与⊙Q相外切时,如答图1所示:

设切点为M,则PQ=PM+QM=AP+QC=AP+(BC-BQ)=x+(13-y)=13+x-y;
∵PQ=BQ,
∴13+x-y=y,即2y-x-13=0
将y=
(x2+25)代入上式得:
(x2+25)-x-13=0,
解此分式方程得:x=
,
经检验,x=
是原方程的解且符合题意.
∴x=
.
(3)按照题意画出图形,如答图2所示,连接QE.

∵EF=EC,EF⊥PQ,EC⊥QC,∴∠1=∠2(角平分线性质).
∵PQ=BQ,∴∠3=∠4,
而∠1+∠2=∠3+∠4(三角形外角性质),∴∠1=∠3.
又∵矩形ABCD,∴AD∥BC,∴∠3=∠5,
∴∠1=∠5,又∵∠C=∠A=90°,
∴△CEQ∽△ABP,
∴
=
,即
=
,化简得:4x+5y=65,
将y=
(x2+25)代入上式得:4x+
(x2+25)=65,
解此分式方程得:x=
,
经检验,x=
是原方程的解且符合题意,
∴x=
.
∵MQ是线段BP的垂直平分线,
∴BQ=PQ,BM=
| 1 |
| 2 |
∴∠MBQ+∠BQM=90°,
∵∠ABP+∠MBQ=90°,∴∠ABP=∠BQM,
又∵∠A=∠BMQ=90°,
∴△ABP∽△MQB,
∴
| BP |
| BQ |
| AP |
| BM |
| BP |
| y |
| x | ||
|
| 1 |
| 2x |
| 1 |
| 2x |
当点Q与C重合时,BQ=PQ=13,在Rt△PQD中,由勾股定理定理得:PQ2=QD2+PD2,即132=52+(13-x)2,解得x=1;
又AP≤AD=13,∴x的取值范围为:1≤x≤13.
∴y=
| 1 |
| 2x |
(2)当⊙P与⊙Q相外切时,如答图1所示:

设切点为M,则PQ=PM+QM=AP+QC=AP+(BC-BQ)=x+(13-y)=13+x-y;
∵PQ=BQ,
∴13+x-y=y,即2y-x-13=0
将y=
| 1 |
| 2x |
| 1 |
| x |
解此分式方程得:x=
| 25 |
| 13 |
经检验,x=
| 25 |
| 13 |
∴x=
| 25 |
| 13 |
(3)按照题意画出图形,如答图2所示,连接QE.

∵EF=EC,EF⊥PQ,EC⊥QC,∴∠1=∠2(角平分线性质).
∵PQ=BQ,∴∠3=∠4,
而∠1+∠2=∠3+∠4(三角形外角性质),∴∠1=∠3.
又∵矩形ABCD,∴AD∥BC,∴∠3=∠5,
∴∠1=∠5,又∵∠C=∠A=90°,
∴△CEQ∽△ABP,
∴
| CQ |
| AP |
| EC |
| AB |
| 13-y |
| x |
| 4 |
| 5 |
将y=
| 1 |
| 2x |
| 5 |
| 2x |
解此分式方程得:x=
65±10
| ||
| 13 |
经检验,x=
65±10
| ||
| 13 |
∴x=
65±10
| ||
| 13 |
点评:本题是中考压轴题,难度较大.试题的难点在于:其一,所考查的知识点众多,包括相似三角形的判定与性质、矩形的性质、勾股定理、圆的位置关系、角平分线的性质、垂直平分线的性质、解分式方程与一元二次方程等,对数学能力要求很高;其二,试题计算量较大,需要仔细认真计算,避免出错.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
(2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )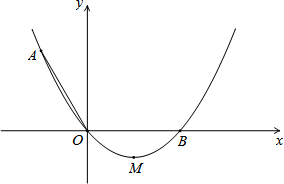 (2013•上海)如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.
(2013•上海)如图,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0),经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=120°.