题目内容
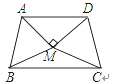
【题目】如图,△ABM与△CDM是两个全等的等边三角形,MA⊥MD.有下列四个结论:(1)∠MBC=25°;(2)∠ADC+∠ABC=180°;(3)直线MB垂直平分线段CD;(4)四边形ABCD是轴对称图形.其中正确结论的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】(1)∵△ABM≌△CDM,△ABM、△CDM都是等边三角形,
∴∠ABM=∠AMB=∠BAM=∠CMD=∠CDM=∠DCM=60°,AB=BM=AM=CD=CM=DM,
又∵MA⊥MD,
∴∠AMD=90°,
∴∠BMC=360°60°6090°=150°,
又∵BM=CM,
∴∠MBC=∠MCB=15°;
(2)∵AM⊥DM,
∴∠AMD=90°,
又∵AM=DM,
∴∠MDA=∠MAD=45°,
∴∠ADC=45°+60°=105°,
∠ABC=60°+15°=75°,
∴∠ADC+∠ABC=180°;
(3)延长BM交CD于N,
∵∠NMC是△MBC的外角,
∴∠NMC=15°+15°=30°,
∴BM所在的直线是△CDM的角平分线,
又∵CM=DM,
∴BM所在的直线垂直平分CD;
(4)根据(2)同理可求∠DAB=105°,∠BCD=75°,
∴∠DAB+∠ABC=180°,
∴AD∥BC,
又∵AB=CD,
∴四边形ABCD是等腰梯形,
∴四边形ABCD是轴对称图形。
故(2)(3)(4)正确。
故选C.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .