��Ŀ����
��2005•���ݣ���ͼ���ھ���ABCD�У�AB=3��BC=2����A������Ϊ��1��0������CDΪֱ�����ھ���AB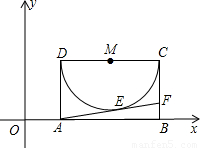 CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N��
CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N����1�����A��C����ֱ�ߵĽ���ʽ��
��2������N�ڰ�ԲM��ʱ����a��ȡֵ��Χ��
��3������A����M�����߽�BC�ڵ�F��EΪ�е㣬���Ե�A��F��BΪ���������������C��N��MΪ���������������ʱ�����N�����꣮
���𰸡���������1�����ݾ��ε����ʼ�A����������C�����꣬�ٸ���A��C����������ô���ϵ�������������A��C����ֱ�ߵĽ���ʽ��
��2������ABCD�У�AB=3��BC=2����A������Ϊ��1��0���������B��D��M��E������꣬�����������������ύ��A��B����ʿ���������ߵĽ���ʽ�����ݽ���ʽ�����N�����꣬�������ߡ���Բ����Գƿ�֪�������ߵĶ����ڹ���M����CD��ֱ��ֱ���ϣ��ֵ�N�ڰ�Բ�ڣ��������a��ȡֵ��Χ��
��3���������ߵ����ʶ��������εı߳������ɶ�������������ߵij�����Ϊ�ڡ�ABF���CMN��Ϊֱ�������Σ���Ӧ������������ۼ���ABF�ס�CMN����ABF�ס�NMC��ͬʱ������ʱ��Ҫ���ǵ�N��CD���·����Ϸ��������
����⣺��1����Ϊ�ھ���ABCD�У�AB=3��BC=2����A������Ϊ��1��0����
����B��4��0����C��4��2����
���A��C�����ֱ�߽���ʽΪy=kx+b��
��A��C�������� ��
��
��� ��
��
�ʹ���A��C��ֱ�ߵĽ���ʽΪy= x-
x- ��
��
��2���������߹�A��B���㣬���������ߵĽ���ʽΪy=a��x-1����x-4����
�����ã�y=ax2-5ax+4a��
�ඥ��N������Ϊ�� ��-
��- ����
����
�������ߡ���Բ����Գƿ�֪�������ߵĶ����ڹ���M����CD��ֱ��ֱ���ϣ��ֵ�N�ڰ�Բ�ڣ�
 ��-
��- ��2��
��2��
���������ʽ����- ��a��-
��a��- ��
��
��3����EF=x����CF=x��BF=2-x��AF=2+x��AB=3��
��Rt��ABF�У��ɹ��ɶ���AB2+BF2=AF2��
��x= ��BF=
��BF= ��
��
���ɡ�ABF�ס�CMN�ã� =
= ����MN=
����MN= =
= ��
��
����N��CD���·�ʱ����- =2-
=2- =
= �����N1��
�����N1�� ��
�� ����
����
����N��CD���Ϸ�ʱ����- =2+
=2+ =
= �����N 2��
�����N 2�� ��
�� ����
����
���ɡ�ABF�ס�NMC�ã� =
= ��MN=
��MN= =
= ��
��
����N��CD���·�ʱ����- =2-
=2- =-
=- �����N3��
�����N3�� ��
�� ����
����
����N��CD���Ϸ�ʱ����- =2+
=2+ =
= �����N4��
�����N4�� ��
�� ����
����
����������Ƚϸ��ӣ��ۺ��Խ�ǿ���ۺϿ�����Բ��һ�κ��������κ��������ʣ���һ���ѶȽϴ����Ŀ��
��2������ABCD�У�AB=3��BC=2����A������Ϊ��1��0���������B��D��M��E������꣬�����������������ύ��A��B����ʿ���������ߵĽ���ʽ�����ݽ���ʽ�����N�����꣬�������ߡ���Բ����Գƿ�֪�������ߵĶ����ڹ���M����CD��ֱ��ֱ���ϣ��ֵ�N�ڰ�Բ�ڣ��������a��ȡֵ��Χ��
��3���������ߵ����ʶ��������εı߳������ɶ�������������ߵij�����Ϊ�ڡ�ABF���CMN��Ϊֱ�������Σ���Ӧ������������ۼ���ABF�ס�CMN����ABF�ס�NMC��ͬʱ������ʱ��Ҫ���ǵ�N��CD���·����Ϸ��������
����⣺��1����Ϊ�ھ���ABCD�У�AB=3��BC=2����A������Ϊ��1��0����
����B��4��0����C��4��2����
���A��C�����ֱ�߽���ʽΪy=kx+b��
��A��C��������
 ��
�����
 ��
���ʹ���A��C��ֱ�ߵĽ���ʽΪy=
 x-
x- ��
����2���������߹�A��B���㣬���������ߵĽ���ʽΪy=a��x-1����x-4����
�����ã�y=ax2-5ax+4a��
�ඥ��N������Ϊ��
 ��-
��- ����
�����������ߡ���Բ����Գƿ�֪�������ߵĶ����ڹ���M����CD��ֱ��ֱ���ϣ��ֵ�N�ڰ�Բ�ڣ�
 ��-
��- ��2��
��2�����������ʽ����-
 ��a��-
��a��- ��
����3����EF=x����CF=x��BF=2-x��AF=2+x��AB=3��
��Rt��ABF�У��ɹ��ɶ���AB2+BF2=AF2��
��x=
 ��BF=
��BF= ��
�����ɡ�ABF�ס�CMN�ã�
 =
= ����MN=
����MN= =
= ��
������N��CD���·�ʱ����-
 =2-
=2- =
= �����N1��
�����N1�� ��
�� ����
��������N��CD���Ϸ�ʱ����-
 =2+
=2+ =
= �����N 2��
�����N 2�� ��
�� ����
�������ɡ�ABF�ס�NMC�ã�
 =
= ��MN=
��MN= =
= ��
������N��CD���·�ʱ����-
 =2-
=2- =-
=- �����N3��
�����N3�� ��
�� ����
��������N��CD���Ϸ�ʱ����-
 =2+
=2+ =
= �����N4��
�����N4�� ��
�� ����
��������������Ƚϸ��ӣ��ۺ��Խ�ǿ���ۺϿ�����Բ��һ�κ��������κ��������ʣ���һ���ѶȽϴ����Ŀ��

��ϰ��ϵ�д�
 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
�����Ŀ
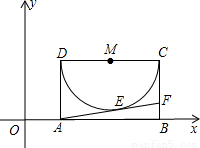 CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N��
CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N��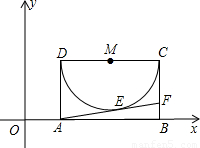 CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N��
CD������Բ����MΪԲ�ģ����A��B���������ߵĽ���ʽΪy=ax2+bx+c������Ϊ��N��


