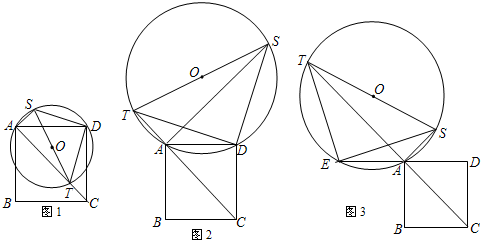
题目内容

已知O为?ABCD对角线的交点，且△AOB的周长比△BOC的周长多
2
3
，则CD-AD的值为（　　）
A、
2
3
B、
3
2
C、2
D、3
分析：因为平行四边形两组对边分别相等，平行四边形的对角线互相平分，所以由△AOB的周长比△BOC的周长多
2
3
，可得AB-BC=
2
3
，所以CD-AD就可以求出了．
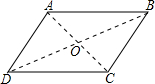解答：精英家教网解：如图，在?ABCD中，AB=CD，AD=CB，OA=OC，
而△AOB的周长比△BOC的周长多
2
3
，
∴AB-BC=
2
3
，
∴CD-AD=
2
3
．
故选A．
点评：此题主要考查平行四边形的性质：平行四边形两组对边分别相等；平行四边形的对角线互相平分．
练习册系列答案
相关题目
在探究矩形的性质时，小明得到了一个有趣的结论：矩形两条对角线的平方和等于四条边的平方和．如图1，在矩形ABCD中，由勾股定理，得AC2=AB2+BC2，BD2=AB2+AD2，又CD=AB，AD=BC，所以AC2+BD2=AB2+BC2+CD2+AD2=2（AB2+BC2）．
小亮对菱形进行了探究，也得到了同样的结论，于是小亮猜想：任意平行四边形两条对角线的平方和等于四条边的平方和．请你解决下列问题：
（1）如图2，已知：四边形ABCD是菱形，求证：AC2+BD2=2（AB2+BC2）；
（2）你认为小亮的猜想是否成立，如果成立，请利用图3给出证明；如果不成立，请举反例说明；
（3）如图4，在△ABC中，BC、AC、AB的长分别为a、b、c，AD是BC边上的中线．试求AD的长．（结果用a，b，c表示）
精英家教网
实验与探究：
（1）在图1，2，3中，已知平行四边形ABCD的三个顶点A，B，D的坐标（如图所示），求出图1，2，3中的第四个顶点C的坐标，已求出图1中顶点C的坐标是（5，2），图2，3中顶点C的坐标分别是
 
，
 
；
精英家教网
（2）在图4中，平行四边形ABCD的顶点A，B，D的坐标（如图所示），求出顶点C的坐标（C点坐标用含a，b，c，d，e，f的代数式表示）；
精英家教网
归纳与发现：
（3）通过对图1，2，3，4的观察和顶点C的坐标的探究，你会发现：无论平行四边形ABCD处于直角坐标系中哪个位置，当其顶点坐标为A（a，b），B（c，d），C（m，n），D（e，f）（如图4）时，则四个顶点的横坐标a，c，m，e之间的等量关系为
 
；纵坐标b，d，n，f之间的等量关系为
 

（不必证明）；运用与推广：
（4）在同一直角坐标系中有抛物线y=x2-（5c-3）x-c和三个点G(-
1
2
c，
5
2
c)，S(
1
2
c，
9
2
c)，H（2c，0）（其中c＞0）．问当c为何值时，该抛物线上存在点P，使得以G，S，H，P为顶点的四边形是平行四边形？并求出所有符合条件的P点坐标．
（2011•临川区模拟）如图，已知正方形纸片ABCD，首先将正方形纸片对折，使AB与CD重合，折痕为EF，再沿直线CG折叠，使B点落在EF上，对应点为B′，连接A B′、D B′，则下列结论正确的是
①②③
①②③
．（多填或错填得0分，少填酌情给分）
①EF平分线段GC；
②△GHB′是等边三角形；
③∠GAB′=75°；
④图中等腰三角形（等边三角形除外）共有4个．
（2012•邗江区一模）已知：正方形ABCD的边长为4，⊙O交正方形ABCD的对角线AC所在直线于点T，连接TO交⊙O于点S．

（1）如图1，当⊙O经过A、D两点且圆心O在正方形ABCD内部时，连接DT、DS．
①试判断线段DT、DS的数量关系和位置关系；    
②求AS+AT的值；
（2）如图2，当⊙O经过A、D两点且圆心O在正方形ABCD外部时，连接DT、DS．求AS-AT的值；
（3）如图3，延长DA到点E，使AE=AD，当⊙O经过A、E两点时，连接ET、ES．根据（1）、（2）计算，通过观察、分析，对线段
AS、AT的数量关系提出问题并解答．
已知平行四边形ABCD的面积为10cm2，一条边长AD=5cm，则对边AD与BC之间的距离为
2
2
cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网