题目内容
设a,b,c是△ABC的三条边,关于x的方程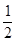 x2+
x2+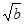 x+c-
x+c-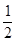 a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状.
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
【答案】
(1)∵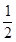 x2+
x2+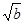 x+c-
x+c-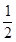 a=0有两个相等的实数根,
a=0有两个相等的实数根,
∴△=(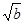 )2-4×
)2-4×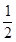 (c-
(c-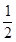 a)=0,
a)=0,
整理得a+b-2c=0 ①,
又∵3cx+2b=2a的根为x=0,
∴a=b ②,
把②代入①得a=c,
∴a=b=c,
∴△ABC为等边三角形;
(2)a,b是方程x2+mx-3m=0的两个根,
∴方程x2+mx-3m=0有两个相等的实数根
∴△=m2-4×(-3m)=0,
即m2+12m=0,
∴m1=0,m2=-12.
当m=0时,原方程的解为x=0(不符合题意,舍去),
∴m=-12.
【解析】(1)因为方程有两个相等的实数根即△=0,由△=0可以得到一个关于a,b的方程,再结合方程3cx+2b=2a的根为x=0,代入即可得到一关于a,b的方程,联立即可得到关于a,b的方程组,可求出a,b的关系式;
(2)根据(1)求出的a,b的值,可以关于m的方程,解方程即可求出m

练习册系列答案
相关题目
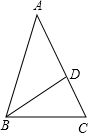 如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.
如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.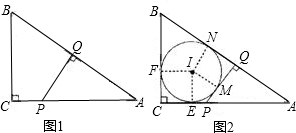
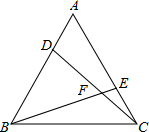 如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.
如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.