Question

【题目】在平面直角坐标系中，已知A（a，0），B（0，b）且a，b满足，

点P在线段AB上（含端点）的一点，连接OP。

（1）若AB=，且△OBP是以OB为腰长的等腰三角形，求BP的长；

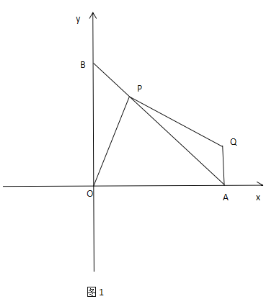
（2）如图1，过点A作AQ⊥x轴（Q在x轴上方），且满足∠OPQ=90°，求证：OP=PQ；

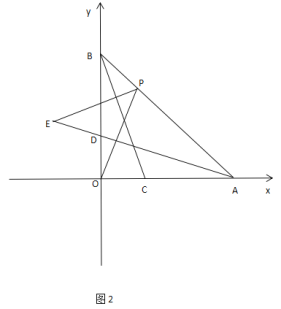
（3）如图2，C,D分别为OA,OB上的两点，且OC=OD，点P满足OP⊥AD，过点P作

PE⊥BC交AD的延长线于点E，试探究AE,OP,PE之间的数量关系，并给出证明。

Answer 1

【答案】（1）6或 （2）证明见解析 （3）答案见解析

【解析】

（1）根据已知求出A与B点的坐标，分别讨论当OB=OP=6时，当OB=BP时求出BP即可；

（2）过点P作PNOA，过点P作PMAQ交延长线于点M，通过证明四边形PNAM为矩形得出PM=AN，再求出，根据得出90°，再证明PNOPMQ即可证明OP=PQ；

（3）过点A作AQX轴与EP延长线交于点Q，证明BOCAOD，则有，根据两锐角互余证明，根据平行得出角相等，则，证明AOPAQP，得出OP=PQ，则可证AE=PE+OP.

解：A（a，0），B（0，b）且a，b满足

∴

则

∴a=6,b=6

故A（6，0），B（0，6）

（1）当OB=OP=6时，

∴此时P点与A点重合，即BP=AB=

当OB=BP时，即BP=6

∴BP=6或；

（2）过点P作PNOA，过点P作PMAQ交延长线于点M

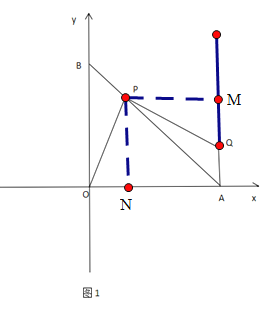
轴，PMAM

°

∴四边形PNAM为矩形，即PM=AN

又

∴为等腰直角三角形，即45°

∴为等腰直角三角形，即

∴

°

∴90°

又

在PNO和PMQ中

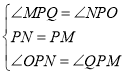
∴PNOPMQ

∴OP=PQ；

（3）AE=PE+OP，理由如下：

过点A作AQX轴与EP延长线交于点Q

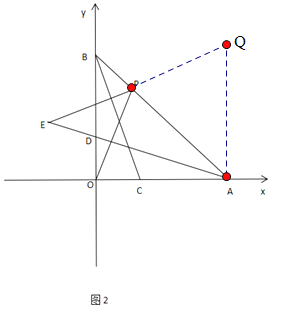
在BOC和AOD中

∴BOCAOD

∴

令

∴

故

轴

∴

在AOP和AQP中

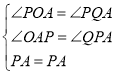
∴AOPAQP

∴OP=PQ

∴AE=PE+OP