题目内容
|

【小题1】赛道的长度是_________m,甲船的速度是________m/s;
【小题2】分别求出甲船在0≤t≤30和30<t≤60时,y关于t的函数关系式;
【小题3】求出乙船由B2到达A2的时间,并在图16-2中画出乙船在3 分钟内的函数图象
【小题4】请你根据(3)中所画的图象直接判断,若从甲、乙两船同时开始出发到3分钟为止,甲、乙共相遇了几次?
【小题1】90,3
【小题2】当0≤t≤30时,y=90-3t , ……………………4分
当30<t≤60时, y=3t-90 . ……………………6分
【小题3】因为赛道的长度为90米,乙的速度为2米/秒,
所以乙船由B2到达A2的时间为45秒; ……………………7分
乙船在3分钟内的函数图象如图5所示:

【小题4】从上图可知甲、乙共相遇5次. ……………………9分解析:
(1)由函数图象可知赛道长为90米,甲船的速度为90÷30=3m/s
(2)设甲船y关于t的函数关系式为
 ,
,当0≤t≤30时,
把(30,0)(0,90)分别代入得
 ,解得
,解得 ,此时y=90-3t;
,此时y=90-3t;当30<t≤60时,把(30,0)(60,90)分别代入得
 ,解得
,解得 ,
,此时y=3t-90。
(3)画图像可知甲乙两船相遇5次。

练习册系列答案
相关题目
|
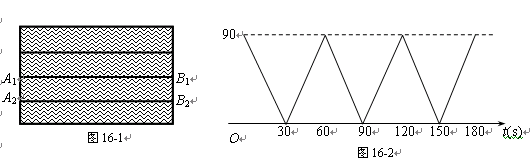
1.赛道的长度是_________m,甲船的速度是________m/s;
2.分别求出甲船在0≤t≤30和30<t≤60时,y关于t的函数关系式;
3.求出乙船由B2到达A2的时间,并在图16-2中画出乙船在3 分钟内的函数图象
4.请你根据(3)中所画的图象直接判断,若从甲、乙两船同时开始出发到3分钟为止,甲、乙共相遇了几次?
(7分)我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你学过的特殊四边形中是勾股四边形的两种图形的名称 , ;
(2)如图16(1),已知格点(小正方形的顶点)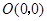 ,
,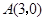 ,
,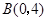 ,请你画出
,请你画出
以格点为顶点,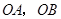 为勾股边且对角线相等的勾股四边形
为勾股边且对角线相等的勾股四边形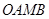 ;
;
 |
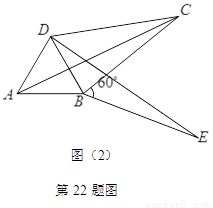
(3)如图16(2),将 绕顶点
绕顶点 按顺时针方向旋转
按顺时针方向旋转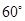 ,得到
,得到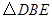 ,连结
,连结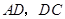 ,
,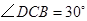 .求证:
.求证: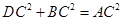 ,即四边形
,即四边形 是勾股四边形
是勾股四边形