题目内容
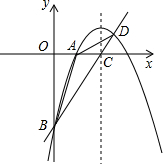 (2012•郯城县一模)如图,已知抛物线y=ax2+4x+c经过A(2,0)、B(0,-6)两点,其对称轴与x轴交于点C.
(2012•郯城县一模)如图,已知抛物线y=ax2+4x+c经过A(2,0)、B(0,-6)两点,其对称轴与x轴交于点C.(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,连接AB、AD,求△ABD的面积;
(3)在该抛物线的对称轴上是否存在点Q,使得△QAB的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
分析:(1)将点A、点B的坐标代入可得出抛物线的解析式,从而得出点C的坐标,利用待定系数法求出直线BC的解析式.
(2)求出点D的坐标,然后根据S△ABD=S△ACD+S△ABC进行计算,即可得出答案.
(3)AB长度固定,只需满足QA+QB最小即可,找点A关于对称轴的对称点A',连接A'B,则A'B与对称轴的交点即是点Q的位置,求出其坐标即可.
(2)求出点D的坐标,然后根据S△ABD=S△ACD+S△ABC进行计算,即可得出答案.
(3)AB长度固定,只需满足QA+QB最小即可,找点A关于对称轴的对称点A',连接A'B,则A'B与对称轴的交点即是点Q的位置,求出其坐标即可.
解答:解:(1)将A(2,0)、B(0,-6)代入抛物线解析式得:
,
解得:
,
故抛物线的解析式为:y=-
x2+4x-6,
其对称轴为:x=4,
故点C的坐标为(4,0),
设直线BC的解析式为y=kx+b,将点B、点C的坐标代入可得:
,
解得:
,
故直线BC的解析式为y=
x-6;
(2)联立直线BC与抛物线的解析式:
,
解得:
或
,
故点D的坐标为(5,
),
则S△ABD=S△ACD+S△ABC=
AC×D纵+
AC×|B纵|=
.
(3)存在点Q,使得△QAB的周长最小;
点A关于抛物线对称轴的对称点为A',连接A'B,则A'B与对称轴的交点即是点Q的位置:
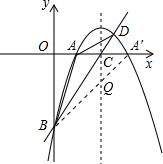
A'坐标为(6,0),B(0,-6),
设直线A'B的解析式为:y=mx+n,代入两点坐标可得:
,
解得:
,
即直线A'B的解析式为y=x-6,
故点Q的坐标为(4,-2).
即存在点Q的坐标(4,-2)时,使得△QAB的周长最小.
|
解得:
|
故抛物线的解析式为:y=-
| 1 |
| 2 |
其对称轴为:x=4,
故点C的坐标为(4,0),
设直线BC的解析式为y=kx+b,将点B、点C的坐标代入可得:
|
解得:
|
故直线BC的解析式为y=
| 3 |
| 2 |
(2)联立直线BC与抛物线的解析式:
|
解得:
|
|
故点D的坐标为(5,
| 3 |
| 2 |
则S△ABD=S△ACD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
(3)存在点Q,使得△QAB的周长最小;
点A关于抛物线对称轴的对称点为A',连接A'B,则A'B与对称轴的交点即是点Q的位置:

A'坐标为(6,0),B(0,-6),
设直线A'B的解析式为:y=mx+n,代入两点坐标可得:
|
解得:
|
即直线A'B的解析式为y=x-6,
故点Q的坐标为(4,-2).
即存在点Q的坐标(4,-2)时,使得△QAB的周长最小.
点评:本题考查了二次函数综合题,涉及了待定系数法求函数解析式、三角形的面积,及利用轴对称求最短路径的问题,解答第二问需要我们将要求图形的面积分割,第三问的关键是利用轴对称的性质得出点Q的位置,难度较大.

练习册系列答案
相关题目
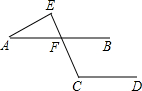 (2012•郯城县一模)如图,已知直线AB∥CD,∠C=100°,∠A=30°,则∠E的度数为( )
(2012•郯城县一模)如图,已知直线AB∥CD,∠C=100°,∠A=30°,则∠E的度数为( ) (2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )
(2012•郯城县一模)如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则cosα=( )