��Ŀ����
����Ŀ����֪��![]() ����
����![]() ��ֱ��
��ֱ��![]() ��һ�����㣨����
��һ�����㣨����![]() �غϣ�����
�غϣ�����![]() ��
��![]() ����һ�����㣬 ����
����һ�����㣬 ����![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ��
��
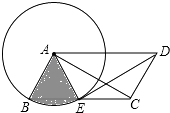
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶�![]() ��ʱ����֤��
��ʱ����֤��![]() ��
��

![]() ��
��![]() �������£��ж�
�������£��ж�![]() �������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
�������ǵĶ������Ƿ�Ϊһ����ֵ�� ����ǣ�������ֵ��������ǣ�˵�����ɣ�
![]() ��ͼ��������
��ͼ��������![]() ���߶�
���߶� ![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ����������������� ��ֱ��д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��
![]() ������
������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��
���ӳ�����ʱ����2���еĽ����Ƿ���Ȼ�������������������ֱ�� д��![]() ֮��Ĺ�ϵ��
֮��Ĺ�ϵ��

���𰸡���1��֤�������������2��![]() �������ǵĶ�����Ϊһ����ֵ����
�������ǵĶ�����Ϊһ����ֵ����![]() ��֤�������������3����������4������������ȷ����Ϊ����EGF-��DEC+��BFG=180��
��֤�������������3����������4������������ȷ����Ϊ����EGF-��DEC+��BFG=180��
��������
��1����������ֱ��ƽ�У��ڴ�����ȣ��ó�![]() ������ֱ��ƽ�У�ͬλ����ȣ��ó�
������ֱ��ƽ�У�ͬλ����ȣ��ó�![]() ������֤��
������֤��![]() ��
��
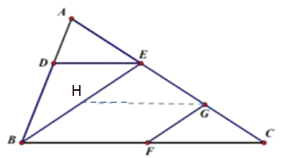
��2������![]() ��
��![]() ��BE�ڵ�H������ƽ�������ʶ�����
��BE�ڵ�H������ƽ�������ʶ�����![]() ��
��![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
��3������![]() ��
��![]() ��BE�ڵ�H���õ�
��BE�ڵ�H���õ�![]() ����Ϊ
����Ϊ![]() ������
������![]() ���õ�
���õ�![]() ��������⣮
��������⣮
��4������![]() ��
��![]() ��BE�ڵ�H���á�DEC=��EGH����Ϊ
��BE�ڵ�H���á�DEC=��EGH����Ϊ![]() ������
������![]() ���Ƶá�HGF+��BFG=180�㣬������⣮
���Ƶá�HGF+��BFG=180�㣬������⣮
��1����![]()
��![]()
��![]()
��![]()
��![]()
��2��![]() �������ǵĶ�����Ϊһ����ֵ����
�������ǵĶ�����Ϊһ����ֵ����![]()
����![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
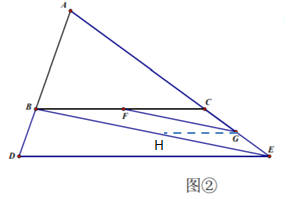
��3������![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() �Ĺ�ϵ�Գ���
�Ĺ�ϵ�Գ���
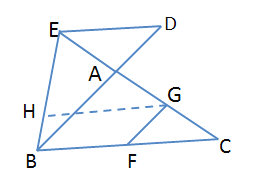
��4������![]() ��
��![]() ��BE�ڵ�H
��BE�ڵ�H
���DEC=��EGH
��![]()
��![]()
���HGF+��BFG=180��
�ߡ�HGF=��EGF-��EGH
���HGF=��EGF-��DEC
���EGF-��DEC+��BFG=180��
�ࣨ2���еĹ�ϵ����������EGF����DEC����BFG֮���ϵΪ����EGF-��DEC+��BFG=180��
�ʴ�Ϊ������������EGF-��DEC+��BFG=180��

����Ŀ����֪A��B�������Ϸֱ��ʾa��b��
(1)��������������
a | 6 | ��6 | ��6 | ��6 | 2 | ��1.5 |
b | 4 | 0 | 4 | ��4 | ��10 | ��1.5 |
A��B����ľ��� |
(2)��A��B�����ľ����Ϊd�����ʣ�d��a��b�к�������ϵ?
(3)���������ҳ����з���������������P��ʹ����5�ͣ�5�ľ���֮��Ϊ10������������Щ�����ĺͣ�
(4)����C��ʾ����Ϊx������C��ʲôλ��ʱ��![]() ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�
ȡ�õ�ֵ��С? ��Сֵ�Ƕ��٣�