题目内容
已知:在△ABC中,AC=a,AB与BC所在直线成45°角,AC与BC所在直线形成的夹角的余弦值为 (即cosC=
(即cosC= ),则AC边上的中线长是________.
),则AC边上的中线长是________.
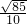 a或
a或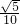 a
a分析:分两种情况:①△ABC的内角∠ABD=45°;②△ABC的外角∠ABD=45°.这两种情况,都可以首先作△ABC的高AD,解直角△ACD与直角△ABD,得到BC的长,再利用余弦定理求解.
解答:
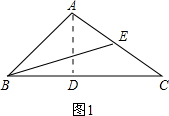 解:分两种情况:
解:分两种情况:①如图1.
作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC=
 ,
,∴CD=
 a,AD=
a,AD= a.
a.∵在直角△ABD中,∠ABD=45°,
∴BD=AD=
 a,
a,∴BC=BD+CD=
 a.
a.在△BCE中,由余弦定理,得
BE2=BC2+EC2-2BC•EC•cosC
=
 a2+
a2+ a2-2×
a2-2× a×
a× a×
a×
=
 a2,
a2,∴BE=
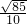 a;
a;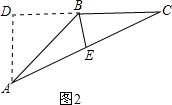 ②如图2.
②如图2.作△ABC的高AD,BE为AC边的中线.
∵在直角△ACD中,AC=a,cosC=
 ,
,∴CD=
 a,AD=
a,AD= a.
a.∵在直角△ABD中,∠ABD=45°,
∴BD=AD=
 a,
a,∴BC=CD-BD=
 a.
a.在△BCE中,由余弦定理,得
BE2=BC2+EC2-2BC•EC•cosC
=
 a2+
a2+ a2-2×
a2-2× a×
a× a×
a×
=
 a2,
a2,∴BE=
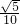 a.
a.综上可知AC边上的中线长是
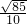 a或
a或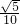 a.
a.故答案为
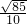 a或
a或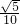 a.
a.点评:本题考查了解直角三角形,勾股定理,余弦定理,有一定难度,进行分类讨论是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上. (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长. 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.