题目内容
 已知正方形ABCD,绕A点顺时针旋转45°得到正方形AB′C′D′,如图所示,如果正方形ABCD边长为1,则四边形的ABED′周长是
已知正方形ABCD,绕A点顺时针旋转45°得到正方形AB′C′D′,如图所示,如果正方形ABCD边长为1,则四边形的ABED′周长是2
| 2 |
2
.| 2 |
分析:作D′H⊥AB于H,EP⊥D′H于P,根据旋转的性质得到AD′=AD=AB=1,∠DAD′=45°,则∠D′AH=45°,可判断△AHD′为等腰直角三角形,根据等腰直角三角形的性质得到AH=D′H=
AD′=
,∠AD′H=45°,于是可计算出BH=PE=1-
,∠ED′P=45°,也得到△PED′为等腰直角三角形,则DE′=
PE=
(1-
)=
-1,D′P=PE=1-
,再计算出BE=PH=D′H-D′P=
-(1-
)=
-1,然后利用周长公式计算四边形的ABED′周长.
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
解答:解: 作D′H⊥AB于H,EP⊥D′H于P,如图,
作D′H⊥AB于H,EP⊥D′H于P,如图,
∵正方形ABCD,绕A点顺时针旋转45°得到正方形AB′C′D′,
∴AD′=AD=AB=1,∠DAD′=45°,
∴∠D′AH=45°,
∴△AHD′为等腰直角三角形,
∴AH=D′H=
AD′=
,∠AD′H=45°,
∴BH=PE=1-
,∠ED′P=45°,
∴△PED′为等腰直角三角形,
∴DE′=
PE=
(1-
)=
-1,D′P=PE=1-
,
∴BE=PH=D′H-D′P=
-(1-
)=
-1,
∴四边形的ABED′周长=AD′+AB+BE+ED′=1+1+
-1+
-1=2
.
故答案为2
.
 作D′H⊥AB于H,EP⊥D′H于P,如图,
作D′H⊥AB于H,EP⊥D′H于P,如图,∵正方形ABCD,绕A点顺时针旋转45°得到正方形AB′C′D′,
∴AD′=AD=AB=1,∠DAD′=45°,
∴∠D′AH=45°,
∴△AHD′为等腰直角三角形,
∴AH=D′H=
| ||
| 2 |
| ||
| 2 |
∴BH=PE=1-
| ||
| 2 |
∴△PED′为等腰直角三角形,
∴DE′=
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∴BE=PH=D′H-D′P=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴四边形的ABED′周长=AD′+AB+BE+ED′=1+1+
| 2 |
| 2 |
| 2 |
故答案为2
| 2 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形的性质以及等腰直角三角形的判定与性质.

练习册系列答案
相关题目
 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2. 已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.
已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.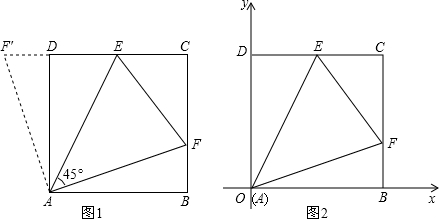
 如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.
如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.