题目内容
如图，A、B两点的坐标分别是A（
，1），B（0，
），则△ABC的面积为
- A.
- B.
- C.
- D.
D
分析：先过A作AC⊥y轴于C，过A作AD⊥x轴于D，结合AB两点的坐标可知AC=OD=，OB=，再利用三角形的面积公式，易求面积．
解答：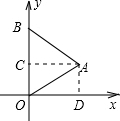
解：如右图所示，过A作AC⊥y轴于C，过A作AD⊥x轴于D，
∵A点坐标是（，1），
∴AD=1，AC=OD=，
∵B点坐标是（0，），
∴OB=，
∴S△ABC=
OB•AC=××=，
故选D．
点评：本题考查了坐标与图形的性质、三角形的面积公式，解题的关键是通过作辅助线，知道AC=OD．
分析：先过A作AC⊥y轴于C，过A作AD⊥x轴于D，结合AB两点的坐标可知AC=OD=
，OB=，再利用三角形的面积公式，易求面积．解答：
解：如右图所示，过A作AC⊥y轴于C，过A作AD⊥x轴于D，∵A点坐标是（
，1），∴AD=1，AC=OD=
，∵B点坐标是（0，
），∴OB=
，∴S△ABC=
OB•AC=××=，故选D．
点评：本题考查了坐标与图形的性质、三角形的面积公式，解题的关键是通过作辅助线，知道AC=OD．
练习册系列答案
名校课堂系列答案
相关题目
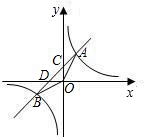如图，一次函数y=kx+b的图象经过第一、二、三象限，且与反比例函数图象相交于A，B两点，与y轴交于点C，与x轴交于点D，OB=
8、如图，从城市A到城市B有三种不同的交通工具：汽车、火车、飞机，除去速度因素，坐飞机的时间最短是因为
20、当你去看电影的时候，你想坐得离屏幕近一些，可是又不想为了看屏幕边缘的镜头不停地转动眼睛．如图所示，点A、B分别为屏幕边缘两点，若你在P点，则视角为∠APB．如果你觉得电影院内P点是观看的最佳位置，可是已经有人坐在那了，那么你会找到一个位置Q，使得在Q、P两点有相同的视角吗？请在图中画出来（保留画图痕迹，不写画法）．
（2013•河北一模）如图，已知直线y=x+4与两坐???轴分别交于A、B两点，⊙C的圆心坐标为 （2，O），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值和最大值分别是