Question

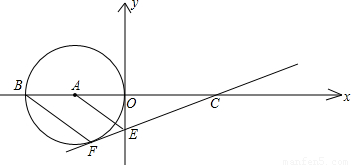
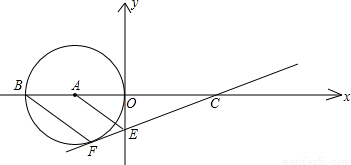
（2006•辽宁）如图，已知A（-1，0），E（0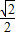，-），以点A为圆心，以AO长为半径的圆交x轴于另一点B，过点B作BF∥AE交⊙A于点F，直线FE交x轴于点C．
（1）求证：直线FC是⊙A的切线；
（2）求点C的坐标及直线FC的解析式；
（3）有一个半径与⊙A的半径相等，且圆心在x轴上运动的⊙P．若⊙P与直线FC相交于M，N两点，是否存在这样的点P，使△PMN是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】分析：（1）连接AF，由于AE∥BF，故∠1=∠3，∠4=∠2，又∵AB=AF，∴∠3=∠4∴∠1=∠2又∵AO=AF，AE=AE
∴△AOE≌△AFE∴∠AFE=∠AOE=90°∴FC是⊙O的切线．
（2）方法由（1）知EF=OE=∵AE∥BF，∴=，∴=∴CE=CO+①（6分）∵OE²+OC²=CE²，∴CE²=（）²+CO²②（7分）由①②解得OC=0（舍去）或OC=2，∴C（2，0）（8分）∵直线FC经过E（0，-），C（2，0）两点，∴直线FC的解析式为y=x-．
解答：（1）证明：连接AF，
∵AE∥BF，
∴∠1=∠3，∠4=∠2，
又∵AB=AF，
∴∠3=∠4，
∴∠1=∠2，
又∵AO=AF，AE=AE，
∴△AOE≌△AFE，
∴∠AFE=∠AOE=90°，
∴FC是⊙O的切线．

（2）解：方法①由（1）知EF=OE=，
∵AE∥BF，
∴=，
∴=，
∴CE=CO+①；
又∵OE²+OC²=CE²，
∴CE²=（）²+CO²②；
由①②解得OC=0（舍去）或OC=2，
∴C（2，0），
∵直线FC经过E（0，-），C（2，0）两点，
设FC的解析式：y=kx+b，
∴，
解得，
∴直线FC的解析式为y=x-．
方法②：
∵CF切⊙A于点F，
∴∠AFC=∠EOC=90°，
又∠ACF=∠OCE，
∴△COE∽△CFA，
∴，
∴，
即CE=CO-①；
又OE²+OC²=CE²，
∴CE²=（）²+CO²②；
由①②解得CO=0（舍去）或CO=2；
∴C（2，0）
（求FC的解析式同上）．
方法③∵AE∥BF，
∴=，
∴=，
∴CE=CO+①，
∵FC切⊙A于点F，
∴∠AFC=∠COE=90°，
∴∠ACE=∠OCE，
∴△COE∽△CFA，
∴=，
∴=，
∴CE=CO-②．
由①②解得：CO=2，
∴C（2，0），
（求FC的解析式同上）．

（3）解：存在：
当点P在点C左侧时，若∠MPN=90°，过点P作PE⊥MN于点E，
∵∠MPN=90°，PM=PN，
∴PE=PM×cos45°⁼，
∵AF⊥FC，
∴PE∥AF，
∴△CPE∽△CAF，
∴=，
∴=，
∴CP=，
∴PO=-2，
∴P（2-，0）．
当点P在点C右侧P′时，设∠M′P′N′=90°，过点P′作P′Q⊥M′N′于点Q，则P′Q=．
∴P′Q=PE，可知P′与P关于点C中心对称，根据对称性得：
∴OP′=OC+CP′=2+，
∴P′（2+，0），
∴存在这样的点P，使得△PMN为直角三角形，P点坐标（2-，0）或（2+，0）．

点评：本题是一道综合性很强的传统型压轴题，其难度比较恰当，选拔功能较强，解第3小题时要注意分类讨论，这是本题最容易失分的地方．