题目内容
在平面直角坐标系xOy中,二次函数y=2x2+bx+c的图象经过(-1,0)和(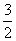 ,0)两点.
,0)两点.
(1)求此二次函数的表达式.
(2)直接写出当-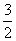 <x<1时,y的取值范围.
<x<1时,y的取值范围.
(3)将一次函数 y=(1-m)x+2的图象向下 平移m个单位后,与二次函数y=2x2+bx+c图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.
平移m个单位后,与二次函数y=2x2+bx+c图象交点的横坐标分别是a和b,其中a<2<b,试求m的取值范围.

 解:(1)由二次函数的图象经过(-1,0)和(
解:(1)由二次函数的图象经过(-1,0)和(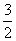 ,0)两点
,0)两点 ,得
,得
 解这个方程组,得
解这个方程组,得
∴此二次函数的表达式为y=2x2-x-3
(2)如图,当x=-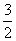 时,y=3,当x=1时y=-2,
时,y=3,当x=1时y=-2,
 又二次函数的顶点坐标是(
又二次函数的顶点坐标是( ).
).
∴当-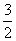 <x<1时y的取值范围是-
<x<1时y的取值范围是- <y<3
<y<3
3)将一次函数 y=(1-m)x+ 2的图象向下平移m个单位后的
2的图象向下平移m个单位后的
一次函数表达式为y=(1-m)x+2-m.
∵y=(1-m)x+2-m与二次函数y=2x2+bx+c图象交点的横坐标为a和b,
∴2x2-x-3=(1-m)x+2-m,整理得2x2+(m-2)x+m-5=0.
∵a<2<b ,∴a≠b,∴△=(m-2)2-4
,∴a≠b,∴△=(m-2)2-4 2(m-5)=(m-6)2+8>0,
2(m-5)=(m-6)2+8>0,
∴m≠1.
∵a和b满足a<2<b,∴如图,当x=2时,(1-m)x+2-m >2x2-x-3,把x=2代入(1-m)x+2-m >2x2-x-3,解得m< ,
,
∴m的取值范围为m< 的全
的全 体实数.
体实数.

练习册系列答案
相关题目
 A.
A.  B.
B.  C.
C.  D.
D. 
 装60台空调,两个安装队同时开工恰好同时安装完成,甲队比乙队平均每天多安装2台空调. 求甲、乙两个安装队平均每天各安装多少台空调.
装60台空调,两个安装队同时开工恰好同时安装完成,甲队比乙队平均每天多安装2台空调. 求甲、乙两个安装队平均每天各安装多少台空调.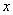 的一元二次方程
的一元二次方程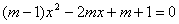 (m>1).
(m>1).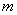 为何整数时,此方程的两个实数根都为正整数?
为何整数时,此方程的两个实数根都为正整数?
 B.
B. C.
C. D.
D.
 的值为0,则x的值等于 .
的值为0,则x的值等于 .  B.
B. C.
C. D.
D.
