题目内容
计算:(1)解一元二次方程:3x2-6x+1=0;(2)(-
| 1 |
| 3 |
| 3 |
分析:(1)用求根公式解即可.(2)注意负整数指数幂和零指数幂的意义.
解答:解:(1)∵a=3,b=-6,c=1,
∴△=(-6)2-4×3×1=24,
所以x=
=
,
即x1=
,x2=
.
(2)原式=9-16÷(-8)+1-2
×
=9+2+1-3=9.
∴△=(-6)2-4×3×1=24,
所以x=
6± 2
| ||
| 2×3 |
2±
| ||
| 3 |
即x1=
2+
| ||
| 3 |
2-
| ||
| 3 |
(2)原式=9-16÷(-8)+1-2
| 3 |
| ||
| 2 |
点评:(1)对于一元二次方程要选择适当的方法去解,一般首选因式分解法,再考虑求根公式,最后用配方法.(2)掌握a-n=
(a≠0),a0=1(a≠0),记住特殊角的三角函数值.
| 1 |
| an |

练习册系列答案
相关题目
 是一元二次方程
是一元二次方程 的两个实数根.
的两个实数根.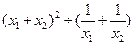 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂. 是一元二次方程
是一元二次方程 的两个实数
的两个实数 根.
根. 的值.考点:实数的运算;零指数幂;负整数指数幂.
的值.考点:实数的运算;零指数幂;负整数指数幂.