题目内容
 如图,△ABC被DE、FG分成面积相等的三部分(即S1=S2=S3),且DE∥FG∥BC,BC=
如图,△ABC被DE、FG分成面积相等的三部分(即S1=S2=S3),且DE∥FG∥BC,BC=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、2-
|
分析:根据△ABC被DE、FG分成面积相等的三部分即可求得DE、FG、BC的比值,设DE=x,FG=
x,BC=
x,根据BC=
即可求得x的值,即可求得FG、DE的长,即解题.
| 2 |
| 3 |
| 6 |
解答:解:∵DE∥FG∥BC,
∴图中所有的三角形均相似,
∴S△ADE:S△AFG:S△ABC=1:2:3,
由相似三角形的性质和面积比可得DE:FG:BC=1:
:
,
设DE=x,FG=
x,BC=
x,
则
x=
,
∴x=
,
∴DE=
,FG=2,
∴FG-DE=2-
.
故选D.
∴图中所有的三角形均相似,
∴S△ADE:S△AFG:S△ABC=1:2:3,
由相似三角形的性质和面积比可得DE:FG:BC=1:
| 2 |
| 3 |
设DE=x,FG=
| 2 |
| 3 |
则
| 3 |
| 6 |
∴x=
| 2 |
∴DE=
| 2 |
∴FG-DE=2-
| 2 |
故选D.
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比值相等的性质,考查了三角形面积的计算,本题中求得DE:FG:BC=1:
:
是解题的关键.
| 2 |
| 3 |

练习册系列答案
相关题目
 如图,△ABC被DE、FG分成面积相等的三部分(即S1=S2=S3),且DE∥FG∥BC,BC=
如图,△ABC被DE、FG分成面积相等的三部分(即S1=S2=S3),且DE∥FG∥BC,BC= ,FG-DE=
,FG-DE=
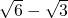
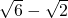
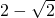
 ,FG-DE=( )
,FG-DE=( )




 ,FG-DE=( )
,FG-DE=( )




 ,FG-DE=( )
,FG-DE=( )



