题目内容
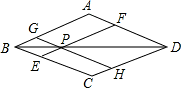 如图,在菱形ABCD中,AB=4,点P是对角线BD上任意一点,过点P作EF∥AB,分别交BC,AD于点E,过点P作GH∥BC,分别交AB,CD于点G,H.则四边形BEPG和四边形PHDF的周长之和是
如图,在菱形ABCD中,AB=4,点P是对角线BD上任意一点,过点P作EF∥AB,分别交BC,AD于点E,过点P作GH∥BC,分别交AB,CD于点G,H.则四边形BEPG和四边形PHDF的周长之和是
- A.8
- B.16
- C.24
- D.32
B
分析:根据题意EF∥AB,GH∥BC及四边形ABCD是菱形可判断出四边形BEPG和四边形PHDF是平行四边形,从而根据平行四边形的对边相等的性质可得出四边形BEPG和四边形PHDF的周长之和等于四边形ABCD的周长.
解答:由题意得:EF∥AB,GH∥BC,AB∥CD,AD∥BC,
∴四边形BEPG和四边形PHDF是平行四边形(两组对边平行),
∴EP=BG,GP=BE,FP=DH,PH=FD,
∴四边形BEPG和四边形PHDF的周长之和=BG+GA+AF+FD+DH+HC+CE+EB=4+4+4+4=16.
故选B.
点评:本题考查了菱形的性质及平行四边形的判定,解答本题的关键是先判断出四边形BEPG和四边形PHDF是平行四边形,然后利用对边相等的知识将所求的线段之和转化.
分析:根据题意EF∥AB,GH∥BC及四边形ABCD是菱形可判断出四边形BEPG和四边形PHDF是平行四边形,从而根据平行四边形的对边相等的性质可得出四边形BEPG和四边形PHDF的周长之和等于四边形ABCD的周长.
解答:由题意得:EF∥AB,GH∥BC,AB∥CD,AD∥BC,
∴四边形BEPG和四边形PHDF是平行四边形(两组对边平行),
∴EP=BG,GP=BE,FP=DH,PH=FD,
∴四边形BEPG和四边形PHDF的周长之和=BG+GA+AF+FD+DH+HC+CE+EB=4+4+4+4=16.
故选B.
点评:本题考查了菱形的性质及平行四边形的判定,解答本题的关键是先判断出四边形BEPG和四边形PHDF是平行四边形,然后利用对边相等的知识将所求的线段之和转化.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
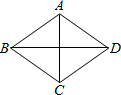 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
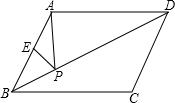
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.