Question

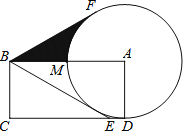
【题目】如图，在矩形ABCD中，E是CD边上的点，且BE=BA=2BC=4，以点A为圆心、AD长为半径作 ⊙A交AB于点M，过点B作⊙A的切线BF，切点为F．

（1）试说明直线BE是⊙A的切线。

（2）求图中阴影部分的面积．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

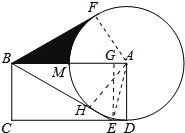
（1）连接AE，过A作AH⊥BE，过E作EG⊥AB，再证明AH=AD即可；

（2）连接AF，则图中阴影部分的面积=直角三角形ABF的面积﹣扇形MAF的面积．

（1连接AE，过A作AH⊥BE，过E作EG⊥AB，则四边形ADEG是矩形．

∵S△ABEBEAHABEG，AB=BE，∴AH=EG．

∵四边形ADEG是矩形，∴AD=EG，∴AH=AD，∴BE是⊙A的切线；

（2）连接AF．

∵BF是⊙A的切线，∴∠BFA=90°

∵BE=BA=2BC=4，∴BC=AD=AF=2，∠BEC=30°．

∵BA∥CD，∴∠HBA=∠BEC=30°．

∵BF，BE是⊙A的切线，∴∠FBA=∠HBA=30°，∴∠BAF=60°，BFAF=，∴图中阴影部分的面积=直角三角形ABF的面积﹣扇形MAF的面积2×=．