Question

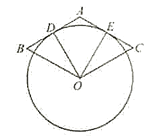
【题目】如图，菱形OABC中，点A在x轴上，顶点C的坐标为(1，)，动点D、E分别在射线OC、OB上，则CE+DE+DB的最小值是____．

Answer 1

【答案】4

【解析】

连接AC，作B关于直线OC的对称点，连接交OC于点D，交OB于点E，此时CE+DE+BD的值最小，结合题意求出CE+DE+DB=，然后，再过点C作CN⊥OA于N点，进一步得出∠=90°，=BF=以及AB=2，最后根据勾股定理求出答案即可.

如图，连接AC，作B关于直线OC的对称点，连接交OC于点D，交OB于点E，此时CE+DE+BD的值最小，

∵四边形OCBA为菱形，

∴AC⊥OB，AO=OC，

即点A与点C关于OB对称，

∴CE=AE，

∴DE+CE=DE+AE=AD，

∵点B与点关于OC对称，

∴，

∴CE+DE+DB=AD+=，

此时，过点C作CN⊥OA于N点，

∵C点坐标为(1，)，

∴ON=1，CN=，

由勾股定理可得：OC=2，

即AB=BC=OA=OC=2，

∴∠CON=60°，

∵四边形COBA为菱形，

∴∠CBA=∠COA=60°，BC∥OA，

∴∠DCB=∠COA=60°，

∵点B与点关于OC对称，

∴∠BFC=90°，，

∴∠=30°，

∴∠=30°+60°=90°，CF=BC=1，

由勾股定理可得：BF=，

∴，

在Rt△中，，

∴CE+DE+DB的最小值为4，

故答案为：4.