题目内容
【题目】如图,已知点A是第一象限内横坐标为2 ![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 . 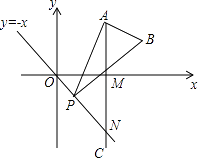
【答案】2 ![]()
【解析】解:由题意可知,OM=2 ![]() ,点N在直线y=﹣x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON=
,点N在直线y=﹣x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,ON= ![]() OM=
OM= ![]() ×2
×2 ![]() =
= ![]() .
.
如答图①所示,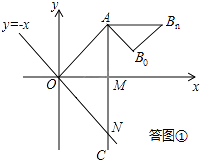
设动点P在O点(起点)时,点B的位置为B0 , 动点P在N点(终点)时,点B的位置为Bn , 连接B0Bn
∵AO⊥AB0 , AN⊥ABn , ∴∠OAC=∠B0ABn ,
又∵AB0=AOtan30°,ABn=ANtan30°,∴AB0:AO=ABn:AN=tan30°(此处也可用30°角的Rt△三边长的关系来求得),
∴△AB0Bn∽△AON,且相似比为tan30°,
∴B0Bn=ONtan30°= ![]() ×
× ![]() =2
=2 ![]() .
.
现在来证明线段B0Bn就是点B运动的路径(或轨迹).
如答图②所示,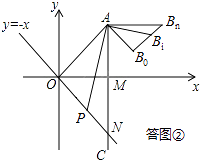
当点P运动至ON上的任一点时,设其对应的点B为Bi , 连接AP,ABi , B0Bi
∵AO⊥AB0 , AP⊥ABi , ∴∠OAP=∠B0ABi ,
又∵AB0=AOtan30°,ABi=APtan30°,∴AB0:AO=ABi:AP,
∴△AB0Bi∽△AOP,∴∠AB0Bi=∠AOP.
又∵△AB0Bn∽△AON,∴∠AB0Bn=∠AOP,
∴∠AB0Bi=∠AB0Bn ,
∴点Bi在线段B0Bn上,即线段B0Bn就是点B运动的路径(或轨迹).
综上所述,点B运动的路径(或轨迹)是线段B0Bn , 其长度为 ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目