题目内容
一小球从某一高空由静止开始下落(不计阻力),设下落的时间为t(s),下落的高度为h(m),已知h与t的函数关系式为h= gt2(其中g为正常数),则函数图象为
gt2(其中g为正常数),则函数图象为
- A.

- B.

- C.

- D.

C
分析:由于h= gt2(其中g为正常数)为二次函数,则其图象为抛物线,而
gt2(其中g为正常数)为二次函数,则其图象为抛物线,而 g>0,根据二次函数的性质得抛物线开口向上,由于t≥0,所以h=
g>0,根据二次函数的性质得抛物线开口向上,由于t≥0,所以h= gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
解答:h= gt2(其中g为正常数)为二次函数,其图象为抛物线,
gt2(其中g为正常数)为二次函数,其图象为抛物线,
∵ g>0,
g>0,
∴抛物线开口向上,
∵t≥0,
∴h= gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
故选C.
点评:本题考查了二次函数的应用:根据实际问题得到二次函数的关系式,然后利用二次函数的性质解决问题.也考查了二次函数的图象.
分析:由于h=
 gt2(其中g为正常数)为二次函数,则其图象为抛物线,而
gt2(其中g为正常数)为二次函数,则其图象为抛物线,而 g>0,根据二次函数的性质得抛物线开口向上,由于t≥0,所以h=
g>0,根据二次函数的性质得抛物线开口向上,由于t≥0,所以h= gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.解答:h=
 gt2(其中g为正常数)为二次函数,其图象为抛物线,
gt2(其中g为正常数)为二次函数,其图象为抛物线,∵
 g>0,
g>0,∴抛物线开口向上,
∵t≥0,
∴h=
 gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.
gt2(其中g为正常数)的图象只是抛物线在第一象限的部分.故选C.
点评:本题考查了二次函数的应用:根据实际问题得到二次函数的关系式,然后利用二次函数的性质解决问题.也考查了二次函数的图象.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
我校部分学生参加了2011年全国初中数学竞赛决赛,并取得优异成绩,已知竞赛成绩都是整数,试题满分为140分,参赛学生的成绩分布情况如下:
| 分数段 | 0~19 | 20~39 | 40~59 | 60~79 | 80~99 | 100~119 | 120~140 |
| 人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么范围内?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求此次参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩的中位数落在哪个分数段内?
 的图象上,则k的值为
的图象上,则k的值为







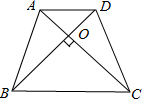 如图.梯形ABCD中,AD∥BC、AB=CD,AC丄BD于点O,∠BAC=60°,若BC=
如图.梯形ABCD中,AD∥BC、AB=CD,AC丄BD于点O,∠BAC=60°,若BC= ,则此梯形的面积为
,则此梯形的面积为

 如图,P是△ABC的BC边上的一点,且BP=PA=AC=PC,则∠B的度数为
如图,P是△ABC的BC边上的一点,且BP=PA=AC=PC,则∠B的度数为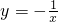 图象上,则
图象上,则