Question

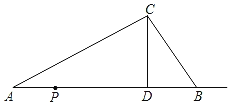
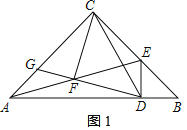
【题目】如图，在△ABC中，∠ACB=90° ,AC=BC=4 点D是边AB上的动点(点D与点A、B不重合)，过点D作DE⊥AB交射线BC于点E，联结AE,点F是AE的中点，过点D、F作直线，交AC于点G,联结CF、CD.

(1)当点E在边BC上，设DB=, CE=

①写出关于的函数关系式及定义域；

②判断△CDF的形状，并给出证明;

(2)如果AE=，求DG的长.

Answer 1

【答案】（1）①y=4-x（0＜x≤2）；②等腰直角三角形；证明见解析；（2）或

【解析】

（1）①先证△DEB为等腰直角三角形，设DB=x，CE=y知EB=x，由EB+CE=4知x+y=4，从而得出答案；②由∠ADE=90°，点F是AE的中点知CF=AF=AE，DF=AF=AE，据此得出CF=DF，再由∠CFE=2∠CAE，∠EFD=2∠EAD知∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD，结合∠CAB=45°知∠CFD=90°，据此可得答案；

（2）分点E在BC上和BC延长线上两种情况，分别求出DF、GF的长，从而得出答案．

解：（1）①∵∠ACB=90°，AC=BC=4，

∴AB=4，∠B=∠BAC=45°，

又∵DE⊥AB，

∴△DEB为等腰直角三角形，

∵DB=x，CE=y，

∴EB=x，

又∵EB+CE=4，

∴x+y=4，

∴y=4-x（0＜x≤2）；

②∵DE⊥AB，∠ACB=90°，

∴∠ADE=90°，

∵点F是AE的中点，

∴CF=AF=AE，DF=AF=AE，

∴CF=DF，

∵∠CFE=2∠CAE，∠EFD=2∠EAD，

∴∠CFD=∠CFE+∠EFD=2∠CAE+2∠EAD=2∠CAD，

∵∠CAB=45°，

∴∠CFD=90°，

∴△CDF是等腰直角三角形；

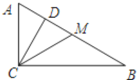
（2）如图1，当点E在BC上时，，AC=4，

在Rt△ACE中，CE=，

则AE=2CE，

∴∠CAE=30°，

又CF=DF=AE=，

在Rt△CFG中，GF=，

∴DG=DF+FG=；

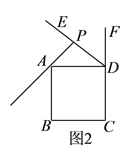
如图2，当点E在BC延长线上时，∠CFD=90°，

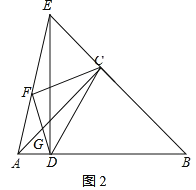
同理可得CF=DF=AE=，

在Rt△CFG中，GF=，

∴DG=DF-FG=．