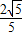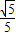题目内容
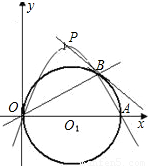
(2007•宿迁)如图,在平面直角坐标系中,⊙O1的直径OA在x轴上,O1A=2,直线OB交⊙O1于点B,∠BOA=30°,P为经过O、B、A三点的抛物线的顶点.(1)求点P的坐标;
(2)求证:PB是⊙O1的切线.
【答案】分析:(1)已知了圆的半径,即可得出A点的坐标;连接O1B,过点B作BC⊥x轴于点C,可在构建的直角三角形O1BC中,根据BO1C的度数和圆的半径求出B点坐标,进而可根据O、A、B三点坐标求出抛物线的解析式,即可得出P点坐标.
(2)证PB是⊙O1的切线,就是证O1B⊥PA,本题主要利用勾股定理进行秋季.可根据O1,P,B三点坐标,分别求出O1P、PB的长,然后用勾股定理进行判断即可.也可求出直线BP与x轴的交点(设为D)的坐标,然后在三角形O1BD中,用勾股定理验证.道理一样.
解答: (1)解:如图,
(1)解:如图,
连接O1B,过点B作BC⊥x轴于点C
∵∠BOA=30°,半径O1A=2,
∴∠BO1C=60°,O1C=1,BC=
∴点B坐标为(3, ).
).
设过O(0,0),A(4,0)两点抛物线解析式为y=ax(x-4),
∵点B(3, )在抛物线上,
)在抛物线上,
∴ =a×3×(3-4),
=a×3×(3-4),
∴a=- ,
,
∴抛物线的解析式为y=- x2+
x2+ x,
x,
∴顶点P的坐标为(2, ).
).
(2)证明:设过P(2, )、B(3,
)、B(3, )两点直线的解析式为y=kx+b,
)两点直线的解析式为y=kx+b,
则
 ,
,
∴直线的解析式为y=- x+2
x+2 ,
,
令y=0,则x=6,
∴直线PB与x轴的交点坐标为D(6,0),
∴OD=6,CD=3,O1D=3+1=4,
∵OB=2
∴BD=2 ,
,
∴O1B2+BD2=22+(2 )2=16=O1D2
)2=16=O1D2
∴O1B2+BD2=O1D2
∴O1B⊥BD,
即PB是⊙O1的切线.
点评:本题考查了二次函数解析式的确定、切线的判断等知识.
(2)证PB是⊙O1的切线,就是证O1B⊥PA,本题主要利用勾股定理进行秋季.可根据O1,P,B三点坐标,分别求出O1P、PB的长,然后用勾股定理进行判断即可.也可求出直线BP与x轴的交点(设为D)的坐标,然后在三角形O1BD中,用勾股定理验证.道理一样.
解答:
 (1)解:如图,
(1)解:如图,连接O1B,过点B作BC⊥x轴于点C
∵∠BOA=30°,半径O1A=2,
∴∠BO1C=60°,O1C=1,BC=

∴点B坐标为(3,
 ).
).设过O(0,0),A(4,0)两点抛物线解析式为y=ax(x-4),
∵点B(3,
 )在抛物线上,
)在抛物线上,∴
 =a×3×(3-4),
=a×3×(3-4),∴a=-
 ,
,∴抛物线的解析式为y=-
 x2+
x2+ x,
x,∴顶点P的坐标为(2,
 ).
).(2)证明:设过P(2,
 )、B(3,
)、B(3, )两点直线的解析式为y=kx+b,
)两点直线的解析式为y=kx+b,则

 ,
,∴直线的解析式为y=-
 x+2
x+2 ,
,令y=0,则x=6,
∴直线PB与x轴的交点坐标为D(6,0),
∴OD=6,CD=3,O1D=3+1=4,
∵OB=2

∴BD=2
 ,
,∴O1B2+BD2=22+(2
 )2=16=O1D2
)2=16=O1D2∴O1B2+BD2=O1D2
∴O1B⊥BD,
即PB是⊙O1的切线.
点评:本题考查了二次函数解析式的确定、切线的判断等知识.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 ,BD与CE、CA分别交于点F、M.
,BD与CE、CA分别交于点F、M.