��Ŀ����
��һ������ȼ�������У��ס�����������ȼ��ʱʣ�ಿ�ֵĸ߶�y�����ף���ȼ��ʱ��x��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ����������⣺
��1���ס�����������ȼ��ǰ�ĸ߶ȷֱ��� ���ӵ�ȼ��ȼ�����õ�ʱ��ֱ���
��2���ֱ���ס�����������ȼ��ʱy��x֮��ĺ�����ϵʽ��
��3��ȼ�նʱ��ʱ���ס�����������ĸ߶���ȣ������Ƕ�ȼ��ʱ���������ʲô�¼����ڣ�����������������ʲôʱ����ڣ��������������ͣ�
��1���ס�����������ȼ��ǰ�ĸ߶ȷֱ��� ���ӵ�ȼ��ȼ�����õ�ʱ��ֱ���
��2���ֱ���ס�����������ȼ��ʱy��x֮��ĺ�����ϵʽ��
��3��ȼ�նʱ��ʱ���ס�����������ĸ߶���ȣ������Ƕ�ȼ��ʱ���������ʲô�¼����ڣ�����������������ʲôʱ����ڣ��������������ͣ�

�⣺��1���ס�����������ȼ��ǰ�ĸ߶ȷֱ���30���ס�25���ף��ӵ�ȼ��ȼ�����õ�ʱ��ֱ���2Сʱ��2.5Сʱ��
��2���������ȼ��ʱy��x֮��ĺ�����ϵʽΪy=k1x+b1��
��ͼ��֪��������ͼ����㣨2��0������0��30����
�� ��
��
���
��y=��15x+30
��������ȼ��ʱy��x֮��ĺ�����ϵʽΪy=k2x+b2��
��ͼ��֪��������ͼ����㣨2.5��0������0��25����
�� ��
��
���
��y=��10x+25��
��3��������é�15x+30=��10x+25�����x=1��
���ԣ���ȼ��1Сʱ��ʱ�ס�����������ĸ߶���ȣ�
�۲�ͼ���֪����0�Qx��1ʱ���������������ߣ�
��1��x��2.5ʱ���������������ͣ�
��2���������ȼ��ʱy��x֮��ĺ�����ϵʽΪy=k1x+b1��
��ͼ��֪��������ͼ����㣨2��0������0��30����
��
 ��
�����

��y=��15x+30
��������ȼ��ʱy��x֮��ĺ�����ϵʽΪy=k2x+b2��
��ͼ��֪��������ͼ����㣨2.5��0������0��25����
��
 ��
�����

��y=��10x+25��
��3��������é�15x+30=��10x+25�����x=1��
���ԣ���ȼ��1Сʱ��ʱ�ס�����������ĸ߶���ȣ�
�۲�ͼ���֪����0�Qx��1ʱ���������������ߣ�
��1��x��2.5ʱ���������������ͣ�

��ϰ��ϵ�д�
 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
�����Ŀ
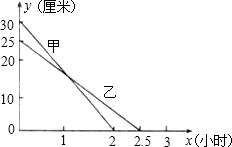 ����ȼ��ʱ��x��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ����������⣺
����ȼ��ʱ��x��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ����������⣺ ����ȼ��ʱ��x��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ����������⣺
����ȼ��ʱ��x��Сʱ��֮��Ĺ�ϵ��ͼ��ʾ�������ͼ�����ṩ����Ϣ����������⣺