题目内容
13.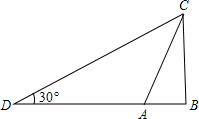 如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=2:1,求山的高度.
如图,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=2:1,求山的高度.
分析 根据山坡AC的坡度设出AB=x,则CB=2x,再根据AD=200米,∠CDB=30°,求出AB,从而求出BC,即可得出山的高度.
解答 解:已知山坡AC的坡度i=2:1,
设AB=x,则CB=2x,又某人在D处测得山顶C的仰角为30°,即∠CDB=30°,
∵AD=200米,
∴tan30°=$\frac{2x}{200+x}$,
解得:x=$\frac{400\sqrt{3}+200}{11}$,
∴BC=2x=2×$\frac{400\sqrt{3}+200}{11}$=$\frac{800\sqrt{3}+400}{11}$(米);
答:山的高度是$\frac{800\sqrt{3}+400}{11}$米.
点评 此题考查了解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,由山坡AC的坡度得出CB和AB的关系,再由三角函数求出AB,继而求出CB.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
3.计算(a-1b2)2的结果是( )
| A. | a-2b4 | B. | a2b2 | C. | a2b4 | D. | a-1b4 |
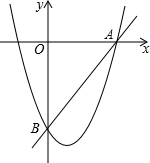 如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.
如图,抛物线y=x2+bx-4分别与x轴正半轴、y轴交于点A、B,且$tan∠OBA=\frac{3}{4}$.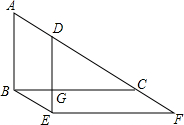 如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,
如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,