Question

（2012•房山区一模）图中的抛物线是函数y=x²+1的图象，把这条抛物线沿射线y=x（x≤0）的方向平移

2

个单位，其函数解析式变为

y=x²+2x+1

；若把抛物线y=x²+1沿射线 y=

1

2

x-1（ x≥0）方向平移

5

个单位，其函数解析式则变为

y=x²-4x+6

．

Answer 1

分析：先求出平移后顶点的坐标，再根据平移不改变二次项系数，即可写出二次函数的顶点式．

解答：解：设函数y=x²+1的顶点为A，则A（0，1）．
把抛物线y=x²+1沿射线y=x（x≤0）的方向平移

2

个单位，设点A的对应点为点B．
∵AB=

2

，OA=1，∠ABO=45°，
∴OB=1，即点B的坐标为（-1，0），
又∵平移前后二次项系数不变，
∴其函数解析式为：y=（x+1）²，即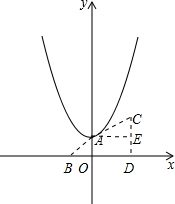y=x²+2x+1；
把抛物线y=x²+1沿射线 y=

1

2

x-1（ x≥0）方向平移

5

个单位，设点A的对应点为点C．
过点C作CD⊥x轴于D，过点A作AE⊥CD于E，则AC=

5

，tan∠CAE=

1

2

，
在直角△CAE中，设CE=x，则AE=2x，
由勾股定理，得AE=2，CE=1，
所以CD=CE+DE=1+1=2，
即点C的坐标为（2，2），
又∵平移前后二次项系数不变，
∴其函数解析式为：y=（x-2）²+2，即y=x²-4x+6．
故答案为：y=x²+2x+1；y=x²-4x+6．

点评：本题考查二次函数的平移问题，用到的知识点为：二次函数的平移，不改变二次项的系数；得到新抛物线的顶点是解决本题的易错点．