题目内容
【题目】已知:直线AB与直线CD交于点O,过点O作OE⊥AB.
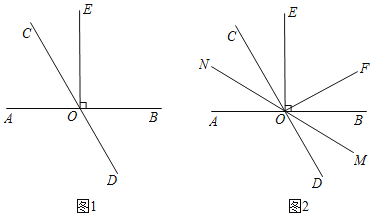
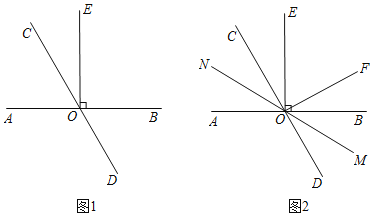
(1)如图1,∠BOC=2∠AOC,求∠COE的度数;
(2)如图2.在(1)的条件下,过点O作OF⊥CD,经过点O画直线MN,满足射线OM平分∠BOD,在不添加任何辅助线的情况下,请直接写出与2∠EOF度数相等的角.
【答案】(1)∠COE=30°;(2)与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.
【解析】
(1)先根据平角的定义可得∠AOC=60![]() ,再利用垂直的定义可得∠AOE=90
,再利用垂直的定义可得∠AOE=90![]() ,从而得结论;
,从而得结论;
(2)根据(1)中∠AOC=60![]() ,分别计算各角的度数,得其中∠EOF=60
,分别计算各角的度数,得其中∠EOF=60![]() ,根据各角的度数可得结论.
,根据各角的度数可得结论.
(1)如图1,∵∠AOC+∠BOC=180![]() ,且∠BOC=2∠AOC,
,且∠BOC=2∠AOC,
∴∠AOC=60![]() ,
,
∵OE⊥AB,
∴∠AOE=90![]() ,
,
∴∠COE=90![]() ﹣60
﹣60![]() =30
=30![]() ;
;
(2)如图2,由(1)知:∠AOC=60![]() ,
,
∵射线OM平分∠BOD,
∴∠BOM=∠DOM=∠AON=∠CON=30![]() ,
,
∵OE⊥AB,OC⊥OF,
∴∠AOE=∠COF=90![]() ,
,
∴∠AOC=∠EOF=60![]() ,
,
∴∠AOD=∠BOC=∠FON=∠EOM=180![]() ﹣60
﹣60![]() =120
=120![]() =2∠EOF,
=2∠EOF,
∴与2∠EOF度数相等的角是:∠AOD,∠BOC,∠FON,∠EOM.

练习册系列答案
相关题目