Question

（2010•萝岗区一模）如图，轮船以30海里/小时的速度从A处向正东方向航行，在A处看小岛B在轮船的北偏东60°的方向，1小时后船航行到C处，在C处看小岛B在北偏西45°的方向，求此时小岛B到C处的距离．（答案用根式表示）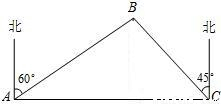

Answer 1

【答案】分析：作高线BD，在直角△ABD与直角△BCD中，可以用BD分别表示出AD于CD的长度，依据AD+CD=AC，即可得到一个关于BD的长的方程，即可求得BD的长．
解答：解：如图，过B点作BD⊥AC于D．（2分）
∴∠DAB=90°-60°=30°．（3分）
∠DCB=90°-45°=45°．（4分）
设BD=x，在Rt△ABD中，AD==x．（6分）
在Rt△BDC中，BD=DC=x（7分）
BC=x．（8分）
又AC=30×1=30，∴．（9分）
解．（10分）
∴（海里）．（11分）
答：此时小岛B到C处的距离为海里．（12分）
点评：一般三角形的问题可以通过作高线转化为直角三角形的问题，进而根据边之间的关系转化为方程的问题．