题目内容
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
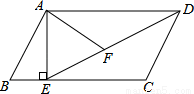
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4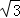 ,求AE的长.
,求AE的长.
(1)证明见解析;(2)6.
【解析】
试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
试题解析:(1)证明:∵四边形ABCD是平行四变形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
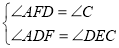
∴△ADF∽△DEC.
(2)【解析】
∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴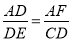
,∴DE=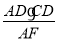 =12.
=12.
在Rt△ADE中,由勾股定理得:AE=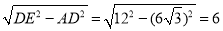 .
.
考点:1.相似三角形的判定与性质;2.勾股定理;3.平行四边形的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目


 C为直角,sinA=
C为直角,sinA= ,则tanB 的值为( ).
,则tanB 的值为( ). B.
B.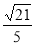 C.
C.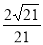 D.
D.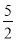
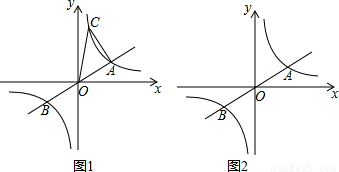
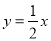 与双曲线
与双曲线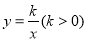 交于
交于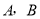 两点,且点
两点,且点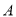 的横坐标为
的横坐标为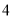 .
.
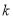 的值;
的值; 上一点
上一点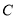 的纵坐标为8,求
的纵坐标为8,求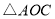 的面积;
的面积;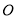 的另一条直线
的另一条直线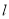 交双曲线
交双曲线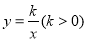 于
于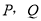 两点(
两点(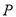 点在第一象限),若由点
点在第一象限),若由点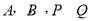 为顶点组成的四边形面积为
为顶点组成的四边形面积为 ,求点
,求点 的坐标.
的坐标.