题目内容
(10分)如图1,O为正方形ABCD的中心,
分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当=30°时,求证:△AOE1为直角三角形.
解:(1)AE1=BF1,证明如下:
∵O为正方形ABCD的中心,∴OA=OB=OD,∴OE=OF
∵△E1OF1是△EOF绕点O逆时针旋转角得到,∴OE1=OF1。
∵ ∠AOB=∠EOF=900, ∴∠E1OA=900-∠F1OA=∠F1OB
![]() OE1=OF1
OE1=OF1
在△E1OA和△F1OB中, ∠E1OA=∠F1OB,∴△E1OA≌△F1OB(SAS)
OA=OB
 ∴ AE1=BF1。
∴ AE1=BF1。
(2)取OE1中点G,连接AG。
∵∠AOD=900,=30° , ∴ ∠E1OA=900-
=60°。
∵OE1=2OA,∴OA=OG,∴ ∠E1OA=∠AGO=∠OAG=60°。
∴ AG=GE1,∴∠GAE1=∠GE1A=30°。∴ ∠E1AO=90°。
∴△AOE1为直角三角形。
解析:略

练习册系列答案
相关题目
 3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
3、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.

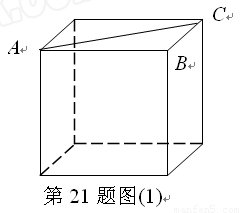

 与平面展开图中
与平面展开图中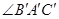 的大小关系?
的大小关系?