题目内容
 如图,直线y=k和双曲线y=
如图,直线y=k和双曲线y=| k |
| x |
| k |
| x |
| AnBn |
| CnBn |
A、
| ||
B、
| ||
C、
| ||
D、1-
|
分析:先根据反比例函数的解析式表示出AnBn、CnBn的值,再根据其比值解答即可.
解答:解:∵A1,A2,…An为连续整数,
又∵直线y=k和双曲线y=
相交于点P的横坐标为1,
∴从A0开始,为1,2,3…,n+1,代入y=
,得yn=
,
即AnBn=
,CnBn=k-
,AnBn÷CnBn=
÷(k-
)=
.
故选C.
又∵直线y=k和双曲线y=
| k |
| x |
∴从A0开始,为1,2,3…,n+1,代入y=
| k |
| x |
| k |
| n+1 |
即AnBn=
| k |
| n+1 |
| k |
| n+1 |
| k |
| n+1 |
| k |
| n+1 |
| 1 |
| n |
故选C.
点评:解答此题要理解两个问题:常函数的概念,直线和双曲线的交点坐标.求出距离,算出它们的比值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
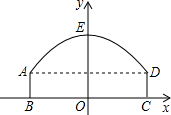 线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.
以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系.y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m. 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=