题目内容
下列命题是真命题的是______
(1)若a+b=0,则a、b一定互为相反数;
(2)若n是自然数,则3n2+6n+1不可能为3的倍数;
(3)若|a|≠|b|,则a+b≠0”;
(4)分数都是有理数;
(5)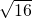 的平方根是±4.
的平方根是±4.
解:若a+b=0,则a、b一定互为相反数,所以(1)正确;若n是自然数,3n2+6n+1=3(n+1)2-2,则3n2+6n+1不可能为3的倍数,所以(2)正确;若|a|≠|b|,则a+b≠0”,所以(3)正确;分数都是有理数,所以(4)正确;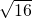 =4,而4的平方根是±2,所以(5)错误.
=4,而4的平方根是±2,所以(5)错误.
故答案为(1)、(2)、(3)、(4).
分析:根据相反数的定义对(1)进行判断;先配方得到3n2+6n+1=3(n+1)2-2,然后根据整数的整除对(2)进行判断;根据绝对值的意义对(3)进行判断;根据有理数的分类对(4)进行判断;根据算术平方根和平方根的定义对(5)进行判断.
点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
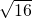 =4,而4的平方根是±2,所以(5)错误.
=4,而4的平方根是±2,所以(5)错误.故答案为(1)、(2)、(3)、(4).
分析:根据相反数的定义对(1)进行判断;先配方得到3n2+6n+1=3(n+1)2-2,然后根据整数的整除对(2)进行判断;根据绝对值的意义对(3)进行判断;根据有理数的分类对(4)进行判断;根据算术平方根和平方根的定义对(5)进行判断.
点评:本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
下列命题是真命题的是( )
A、任意抛掷一只一次性纸杯,杯口朝上的概率为
| ||
B、在一次抽奖活动中,“中奖的概率是
| ||
C、从1至9这九个自然数中任取一个,是2的倍数或是3的倍数的概率是
| ||
D、一运动员投4次篮,有2次投中,则该运动员的投一次篮投中的概率一定是
|

 ”表示抽奖100次就一定会中奖
”表示抽奖100次就一定会中奖
