��Ŀ����
����Ŀ����ͼ��������ABCD��ƽ��ֱ������ϵ�У�AD��BC��x�ᣬAB��DC��y�ᣬx����y��н�Ϊ90������M��N�ֱ���xy���ϣ���A��1��8����B��1��6����C��7��6����D��7��8����

��1�������߶�OB��OD��BD������OBD�������
��2����������ABCD�ڵ�һ��������ÿ��0.5����λ���ȵ��ٶ�����ƽ�ƣ�����������ʱ����OBD������볤����ABCD����������ֱ��д���𰸣�
��3��������ͼ������ OB��OD��OD��BC�ڵ�E����BON��ƽ���ߺ͡�BEO��ƽ���߽��ڵ�F��
�ٵ���BEO�Ķ���Ϊn����BON�Ķ���Ϊmʱ�����OFE�Ķ�����
����ֱ��д����OFE�͡�BOE֮���������ϵ��
���𰸡���1��17����2��![]() ����3���١�EFO��
����3���١�EFO��![]() m+
m+![]() n+90������2��EFO+��BOE��270����
n+90������2��EFO+��BOE��270����
��������
��1���ӳ�DA��y����H����ͼ1��ʾ����AH��y�ᣬȻ������S��OBD��S��ODH��S��ABD��S����AHOB�������ݼ��㼴�ɣ�
��2����S��OBD��S��ODH��S��ABD��S����AHOB��S������ABCD��12�����г�����t�ķ��̣��ⷽ�̼��ý����
��3�����ӳ�CB��y���ڵ�P���ӳ�EF��y���ڵ�G����ͼ2�����ݽ�ƽ���ߵĶ���������ε�������ʽ�ɣ�
�ڸ��ݽ�ƽ���ߵĶ���������ε�������ʿɵá�EFO��90��+![]() (��NOB+��BEO)������ֱ�������ε����ʿɵá�BON+��BEO=90������BOE����һ�����ɵó����ۣ�
(��NOB+��BEO)������ֱ�������ε����ʿɵá�BON+��BEO=90������BOE����һ�����ɵó����ۣ�
�⣺��1���ӳ�DA��y����H����ͼ1��ʾ��
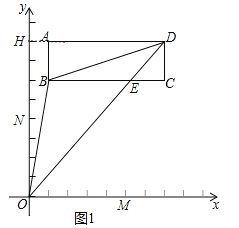
��AH��y�ᣮ
��A��1��8����B��1��6����C��7��6����D��7��8��
��OH��8��DH��7��AH��1��AD��6��AB��2��
��S��OBD��S��ODH��S��ABD��S����AHOB
��![]() ��OH��DH��
��OH��DH��![]() ��AB��AD��
��AB��AD��![]() ����AB+OH����AH
����AB+OH����AH
��![]() ��8��7��
��8��7��![]() ��2��6��
��2��6��![]() ����2+8����1��17��
����2+8����1��17��
��2����S������ABCD��2��6��12��
��S��OBD��S��ODH��S��ABD��S����AHOB��12��
��![]() ����8��0.5t����7��
����8��0.5t����7��![]() ��2��6��
��2��6��![]() ����2+8��0.5t����1��12��
����2+8��0.5t����1��12��
��ã�t��![]() ��
��
��3�����ӳ�CB��y���ڵ�P���ӳ�EF��y���ڵ�G����ͼ2��
��EFƽ�֡�BEO��OFƽ�֡�NOB��
���GOF��![]() ��NOB��
��NOB��![]() m����BEF��
m����BEF��![]() ��BEO��
��BEO��![]() n��
n��
�ߡ�EFO����GOF+��FGO����FGO����GPE+��BEF��
���EFO����GOF+��GPE+��BEF��![]() m+
m+![]() n+90����
n+90����
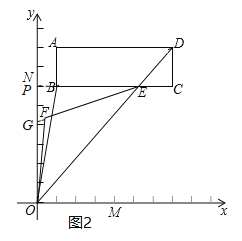
�ڡ�EFƽ�֡�BEO��OFƽ�֡�NOB��
���GOF��![]() ��NOB����BEF��
��NOB����BEF��![]() ��BEO��
��BEO��
�ߡ�EFO����GOF+��FGO����FGO����GPE+��BEF��
���EFO����GOF+��GPE+��BEF��90��+![]() ��NOB+
��NOB+![]() ��BEO��90��+
��BEO��90��+![]() (��NOB+��BEO)��
(��NOB+��BEO)��
�ߡ�BOE��90������BON����BEO��
���BON+��BEO=90������BOE��
���EFO��90��+![]() (90������BOE)��
(90������BOE)��
��2��EFO+��BOE��270����

����Ŀ���������¡�̳���A��B������Ʒ�Ľ��ۺ��ۼ������
��Ʒ �۸� | A | B |
���ۣ�Ԫ/���� | m | m+20 |
�ۼۣ�Ԫ/���� | 160 | 240 |
��֪����2400Ԫ����A����Ʒ����������3000Ԫ����B����Ʒ��������ͬ��
��1����m��ֵ��
��2�����̳��ƻ�ͬʱ������A��B������Ʒ��200�������й���A����Ʒx����ʵ�ʽ���ʱ���������Ҷ�A����Ʒ�ij������µ�a��50��a��70��Ԫ���ۣ����̳�����ͬ����Ʒ���ۼ۲��䣬�̳�������200����Ʒ��������ΪyԪ��
����y����x�ĺ�����ϵʽ��
������A����Ʒ����120�����ٹ���100�����������������Ϣ����Ƴ�ʹ���̳�����������Ľ���������





