题目内容
【题目】如图，在平面直角坐标系中，点A的坐标为（﹣1，0），点B的坐标为（4，0），经过点A点B抛物线y=x2+bx+c与y轴交于点C．
（1）求抛物线的关系式；
（2）△ABC的外接圆与轴交于点D，在抛物线上是否存在点M使S△MBC=S△DBC ， 若存在，请求出点M的坐标．
（3）点P是直线y=﹣x上一个动点，连接PB，PC，当PB+PC+PO最小时，求点P的坐标及其最小值．
【答案】
（1）
解：设抛物线的解析式为y=a（x+1）（x﹣4）．
由题意得可知：a=1．
所以抛物线的解析式为y=x2﹣3x﹣4．
（2）
解：如图所示：过点D作直线DM∥BC，交抛物线与点M和点M′．
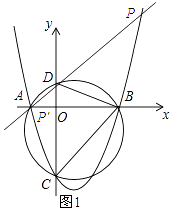
∵DM∥BC，
∴S△MBC=S△DBC．
∵ODOC=OBOA，
∴4OD=4×1，解得DO=1．
∴D（0，1）．
设直线BC的解析式为y=kx+b，将点B和点C的坐标代入得 
，解得k=1，b=﹣4．
∵DM∥BC，
∴直线DM的解析式为y=x+1．
将y=x+1代入y=x2﹣3x﹣4得：x2﹣3x﹣4=x+1，整理得：x2﹣4x﹣5=0，解得x=﹣1或x=5．
当x=﹣1时，y=0，
∴M′的坐标为（﹣1，0）．
当x=5时，y=6．
∴M的坐标为（5，6）．
综上所述，点M的坐标为（﹣1，0）或（5，6）．
（3）
解：如图2所示：△OPC顺时针旋转60°得到△O′C′P′，连结C′P′、PP′、PB，过点C′作C′E⊥x轴，垂足为E．
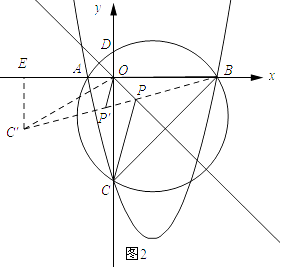
由旋转的性质可知：CP′=CP，OP=OP′，∠POP′=60°．
∴△OPP′为等边三角形．
∴OP=PP′．
∴CP+PB+OP=C′P′+PB+PP′．
∴当点C′P′、PP′\PB在一条直线上时，CP+PB+OP有最小值，最小值=C′B．
∵OP的解析式为y=﹣x，
∴∠POC=45°，
∴∠P′OC′=45°．
∴∠EOC′=30°．
∴EC′= 
OC′=2，EO=2 
．
∴C′（﹣2 ，﹣2）．
设直线C′B的解析式为y=kx+b，则 
，解得k=2﹣ ，b=4 ﹣8．
∴直线C′B的戒形式为y=（2﹣ ）x+4 ﹣8．
将y=﹣x代入得：﹣x=（2﹣ ）x+4 ﹣8，解得x= 
．
∴y= 
．
∴点P的坐标为（ ， ）
∵C′（﹣2 ，﹣2）．
∴BE=4+2 ．
依据勾股定理得：BC′= 
= 
= 
=2 
=2 
+2 
．
所以PB+PC+PO的最小值为2 +2 ．
【解析】（1）设抛物线的解析式为y=a（x+1）（x﹣4），将a=1代入即可；（2）过点D作直线DM∥BC，交抛物线与点M和点M′．则S△MBC=S△DBC ， 利用相交弦定理可求得OD的长，从而得到点D的坐标，然后可求得DM的解析式，接下来再求得y=x+1与y=x2﹣3x﹣4的交点坐标即可；（3）△OPC顺时针旋转60°得到△O′C′P′，连结C′P′、PP′、PB，过点C′作C′E⊥x轴，垂足为E．先证明△OPP′为等边三角形，由两点之间线段最短可知：当点C′P′、PP′\PB在一条直线上时，CP+PB+OP有最小值，最小值=C′B．接下来，在求得C′（﹣2 ，﹣2），然后可求得C′B的解析式为y=（2﹣ ）x+4 ﹣8，然后可求得它与y=﹣x的交点坐标，然后依据勾股定理可求得BC′的值．
【考点精析】本题主要考查了三角形的外接圆与外心的相关知识点，需要掌握过三角形的三个顶点的圆叫做三角形的外接圆，其圆心叫做三角形的外心才能正确解答此题．
