题目内容
在⊙O中，OD⊥弦AB，垂足为C，∠DEB=32°，则∠AOD= 度，∠A= 度．
【答案】分析：由于半径OD⊥AB，根据垂径定理知：D是
的中点，根据同弧所对的圆心角和圆周角的度数关系，即可求得∠AOD的度数，进而可在Rt△OAC中，求出∠A的度数．
解答：解：∵OD⊥弦AB，
∴D是
的中点，
∴∠AOD=2∠DEB=64°，
∴∠A=90°-∠AOD=26°．
故答案为：64，26．
点评：此题主要考查了圆周角定理和垂径定理的综合应用能力．
的中点，根据同弧所对的圆心角和圆周角的度数关系，即可求得∠AOD的度数，进而可在Rt△OAC中，求出∠A的度数．解答：解：∵OD⊥弦AB，
∴D是
的中点，∴∠AOD=2∠DEB=64°，
∴∠A=90°-∠AOD=26°．
故答案为：64，26．
点评：此题主要考查了圆周角定理和垂径定理的综合应用能力．
练习册系列答案
相关题目
如图，已知：在⊙O中，直径AB=4，点E是OA上任意一点，过E作弦CD⊥AB，点F是
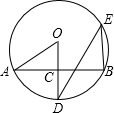在⊙O中，OD⊥弦AB，垂足为C，∠DEB=32°，则∠AOD=
在⊙O中，OD⊥弦AB，垂足为C，∠DEB=32°，则∠AOD=________度，∠A=________度．