Question

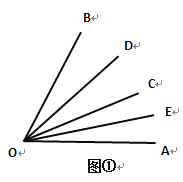
【题目】如图①，(1)∠AOB＝60°，∠BOC＝36°OD平分∠BOC，OE平分∠AOC，则∠EOD＝____度；

（2）若∠AOB＝90°，OD平分∠BOC，OE平分∠AOC，则∠EOD＝__________;

（3）若∠AOB＝α，其它条件同（2），则∠EOD＝_________________.

类比应用：

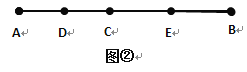
如图②，已知线段AB，C是线段AB上任一点，D、E分别是AC、CB的中点，试猜想DE与AB的数量关系为_____________，并写出求解过程．

Answer 1

【答案】（1）30；（2）45度；（3）α；类比应用：DE=AB，见解析.

【解析】

（1）根据角平分线的定义，∠COD= ∠BOC，∠COE=∠AOC，所以∠EOD=∠AOB，代入数据计算即可；
（2）与（1）的求解与解答思路相同；
（3）与（1）的求解与解答思路相同；
类比应用：把题中的∠AOB换成线段AB，相应的角平分线换成中点即可．

解：(1)∵∠AOB＝60°，∠BOC＝36°

∴∠AOC=24°

∵OD平分∠BOC，OE平分∠AOC，

∴∠DOC=∠BOC=18°,∠COE=∠AOC=12°，

∴∠EOD=∠DOC+∠COE=∠BOC+∠AOC=(∠BOC+∠AOC)=∠AOB，

∵∠AOB=60°，

∴∠EOD=×60°=30°；

(2)同理∠EOD=∠AOB=×90°=45°；

(3)同理∠EOD=∠AOB= ；

类比应用：如图②，∵D是AC的中点，E是BC的中点，

∴DC=AC,EC=BC；

∴DE=AC+BC=(AC+BC)=AB.

故答案为：（1）30；（2）45度；（3）α；类比应用：DE=AB，见解析.