题目内容
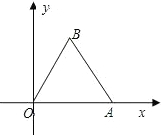
 如图,边长为2的等边△OAB在第一象限,写出B点的坐标,并求过O、A、B三点的二次函数的解析式.
如图,边长为2的等边△OAB在第一象限,写出B点的坐标,并求过O、A、B三点的二次函数的解析式.
 解:作BH⊥OA于H,则OH=1,由勾股定理,得
解:作BH⊥OA于H,则OH=1,由勾股定理,得BH=
 =
= ,
,∴A(2,0),B(1,
 ),
),设过O、A、B三点的二次函数的解析式为y=ax(x-2),
把B(1,
 )代入,得
)代入,得 =a•1•(1-2),
=a•1•(1-2),解得:a=-
 ,
,∴y=-
 x(x-2)=-
x(x-2)=- x2+2
x2+2 x.
x.分析:根据等边三角形的位置,边长求B点坐标,由O、A两点坐标,设抛物线的交点式,将B点坐标代入即可.
点评:本题考查了用待定系数法求函数解析式的方法,同时还考查了方程的解法,勾股定理等知识,难度不大.

练习册系列答案
相关题目
 如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线
如图,边长为2的等边三角形OAB的顶点A在x轴的正半轴上,B点位于第一象限,将△OAB绕点O顺时针旋转30°后,恰好点A落在双曲线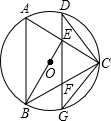 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
 (1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长.
(1997•南京)已知:如图,边长为2的等边三角形ABC,延长BC到D,使CD=BC,延长CB到E,使BE=CB,求△ADE的周长. (2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是
(2013•福州质检)如图,边长为6的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E运动过程中,DF的最小值是