��Ŀ����
����Ŀ��ͼ1��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ�������Σ�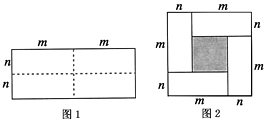
��1���������ֲ�ͬ�ķ�����ͼ2����Ӱ���ֵ������
����1����
����2����
��2���۲�ͼ2����д��������������ʽ����m+n��2 �� ��m-n��2 �� mn֮��ĵ�����ϵ��
��3�����ݣ�2�����еĵ�����ϵ������������⣺
����֪�� ![]() ��
�� ![]() ����
���� ![]() ��ֵ��
��ֵ��
����֪�� ![]() ��
�� ![]() ����
���� ![]() ��ֵ.
��ֵ.
���𰸡�
��1����m��n��2,��m+n��2��4mn
��2����m��n��2����m+n��2��4mn����m��n��2=��m+n��2��4mn
��3���⣺��a��b=5��ab=��6��
�ࣨa+b��2=��a��b��2+4ab=52+4������6��=25��24=1��
�ڽ⣺����֪�ã���a+ ![]() ��2=��a��
��2=��a�� ![]() ��2+4a
��2+4a ![]() =12+8=9��
=12+8=9��
��a��0��a+ ![]() ��0��
��0��
��a+ ![]() =3
=3
���������⣺��1������1����m��n��2��
����2����m+n��2��4mn��
�� 2 ����m��n��2=��m+n��2��4mn��
���Դ��ǣ���m��n��2����m+n��2��4mn����m��n��2=��m+n��2��4mn��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ